모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

🎲 01. 통계학 종류
• 기술통계학(Descriptive Statistics) : 자료를 그래프나 표 또는 몇 개의 숫자로 요약하여, 전반적인 내용을 빠르게 파악하는 기법
• 추측통계학(Inferential Statistics) : 관심의 대상이 되는 모집단에서 일부(표본)를 추출하고, 표본으로부터 관측된 내용(통계량)을 근거로 하여 모집단의 특성(모수)을 추측하고 검정하는 방법
🎲 02. 표본추출(Sampling)
• 모집단(Population) : 정보를 원하는 전체 대상
• 표본(Sample) : 관측하는 모집단의 일부
• 표집단위(Unit; 개체) : 조사의 기본 단위(예: 응답자, 가구, 사업체, 학교)
• 표본추출 프레임 : 표본이 추출될 목록 (예: 전화번호부)
• 전수조사 : 모집단 전체를 조사하는 방법 (예: 인구주택총조사)
• 표본조사 : 모집단의 일부를 조사하는 방법
🎲 03. 모수와 통계량
• 모수(Parameter) : 모집단의 특성치.
- 모총계, 모평균, 모비율, 모분산…
- 모수는 상수(constant)이나 표본조사에서는 그 값을 알 수 없음.
• 통계량(Statistic; 추정량, 추정치) : 표본의 특성치.
- 표본총계, 표본평균, 표본비율, 표본분산 …
- 변수(variable)로서 표본에 따라서 달라짐
- 통계량은 변수기 때문에, 분포를 가짐 -> 표본 분포
🎲 04. 자료의 분류
• 질적자료(qualitative data) = 범주형 자료(categorical data)
- 비계측자료(nonmetric)
- 학년, 성별, 등급 등
- 조사대상을 특성에 따라 범주로 구분하여 측정된 변수
- 사칙연산 불가능
- ① 명목형 자료(Nominal data) : 성별, 직업, 지역 등과 같이 크기나 순서의 의미가 없고 자료값의 이름만 의미를 가짐
- ② 순서형 자료(Ordinal Data): 학년, 순위, 성적등급 등과 같이 기준에 따라 자료값의 순서의 개념이 있음
• 양적자료(quantitative data) = 숫자형 데이터(numerical data)
- 계측데이터(metric)
- 길이, 무게 등과 같이 양적인 수치로 측정되거나 몇 개인가를 세어 측정하는 변수
- 사칙연산 가능
- ① 연속형 자료(continuous data) : 몸무게, 키, 전구수명 등과 같이 셀 수 없는 소수점을 포함하는 자료
- ② 이산형 자료(discrete data) : 자녀의 수, 교통사고건수, 불량품 수 등과 같이 셀 수 있는 정수 형태의 자료
🎲 05. 질적 데이터의 요약
• 질적 데이터 요약 01. 빈도표
- 각 범주에 속한 도수 또는 퍼센트를 나타내는 빈도표, 분할표를 구해 이산형 변수에 대한 분포 파악
# 데이터 전처리
score = pd.read_csv("Score.csv")
score['Dept'] = score['Dept'].astype('str')
score['Gender'] = score['Gender'].astype('str')
Deptlabel = {'1' : 'Stat', '2' : 'Math'}
score['Dept'] = score['Dept'].map(Deptlabel)
Genderlabel = {'1' : '남자', '2' : '여자'}
score['Gender'] = score['Gender'].map(Genderlabel)
score

☑️ crosstab( ) 빈도표
## 2차원 빈도표
## crosstab()(pandas패키지) : 데이터프레임에 적용, 둘 이상의 변수에 대한 교차표를 작성
## pd.crosstab(index=Score["Dept"],columns=Score["Gender"])
## crosstab(index=, columns=, …)
## index : 행(row) 변수 지정
## columns : 열(columns) 변수 지정, columns = “count” 는 1차원 빈도표 출력
## margins : 주변합 계산 출력 여부 지정, 기본값은 False
## normalize : 비율 출력 옵션(“all”,“index”,“columns”)지정, 기본값은 False
## all -> 전체 합에 대한 비율 / index -> 행 합에 대한 비율 / columns -> 열 합에 대한 비율
print(pd.crosstab(index=score['Dept'], columns='count'))
print(pd.crosstab(index=score['Gender'], columns='count'))
print(pd.crosstab(index=score['Dept'], columns=score['Gender']))
print(pd.crosstab(index=score['Dept'], columns=score["Gender"], margins=True))
print(pd.crosstab(index=score['Dept'], columns=score['Gender'], normalize='all'))
print(pd.crosstab(index=score['Dept'], columns=score['Gender'], normalize='index'))
print(pd.crosstab(index=score['Dept'], columns=score['Gender'], normalize='columns'))# 1
col_0 count
Dept
Math 5
Stat 7
# 2
col_0 count
Gender
남자 8
여자 4
# 3
Gender 남자 여자
Dept
Math 3 2
Stat 5 2
# 4
Gender 남자 여자 All
Dept
Math 3 2 5
Stat 5 2 7
All 8 4 12
# 5
Gender 남자 여자
Dept
Math 0.250000 0.166667
Stat 0.416667 0.166667
# 6
Gender 남자 여자
Dept
Math 0.600000 0.400000
Stat 0.714286 0.285714
# 7
Gender 남자 여자
Dept
Math 0.375 0.5
Stat 0.625 0.5
☑️ pivot_table( ) 빈도표
## pivot_table 함수를 이용한 2차원 빈도표(분할표, 교차표) 작성
## Pivot_table()(pandas패키지) : 데이터프레임에 대하여 스프레드 시트 형태의 피봇 테이블을 출력
## Score.pivot_table(index=["Dept"],columns=["Gender"],aggfunc=["count"], margins=True)
## df_name.pivot_table(index=[“ "],columns=[“ "],aggfunc=["count"],margins=True)
## index = : 행 변수 또는 리스트 지정, columns = : 열 변수 또는 리스트 지정
## aggfunc = : 요약변수에 대한 함수 지정
## margins = True : 주변 합계의 출력(기본값은 False)
score.pivot_table(index=['Dept'], columns=['Gender'], aggfunc=['count'], margins = True)
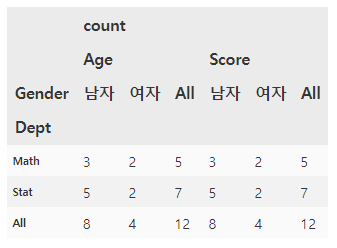
• 질적 데이터 요약 02. 그래프
# 데이터
import matplotlib.pyplot as plt
Drink = pd.read_csv('Drink.csv', encoding = 'euc-kr')
## 집계를 위한 ChartTable 사용
## 원본 데이터는 각 음료수를 섭취한 ID와 Age에 대한 데이터임
## 따라서, groupby() 함수로 이를 집계해서 표현하기 위한 데이터를 만들어줘야 함
ChartTable = Drink.groupby("Drink").size()
ChartTable# ChartTable
Drink
A 35
B 25
C 18
D 30
dtype: int64
☑️ Bar Chart
## 질적변수의 각 범주별 빈도를 막대의 형태로 그린 것
## plot 함수(pandas데이터프레임) : 데이터프레임과 시리즈에 대하여 다양한 plot을 그림
## df_name.plot(data, x, y, kind, …)
## ChartTable.plot(kind='bar',x=ChartTable.index,y=ChartTable.values, title="Drink Preference")
ChartTable.plot(kind='bar',x=ChartTable.index,y=ChartTable.values, title="Drink Preference")

## matplotlib 사용
plt.bar(ChartTable.index,ChartTable.values)
plt.show()

☑️ pie chart
ChartTable.plot(kind='pie',x=ChartTable.index,y=ChartTable.values, title="Drink Preference")

## autopct='%1.1f%%’ : autopct는 부채꼴 안에 표시될 숫자의 형식을 지정
plt.pie(ChartTable.values, labels=ChartTable.index, autopct='%1.1f%%')
plt.show()

☑️ Mosaic Chart
## 다차원 분할표에 대하여 각 범주별 크기를 그래프로 나타낸 것
## mosaic 함수 (statsmodels 패키지)
## mosaic(data, index=None, horizontal =True, …)
## 다차원 분할표 요약에 유용함
## 전반적인 자료 이해에 도움이 됨
# statsmodels 패키지에서 mosaic 불러오기
from statsmodels.graphics.mosaicplot import mosaic
mosaic(Drink,['Age','Drink'])

🎲 06. 양적 데이터의 요약
• 양적 데이터 요약 01. 기술통계량(descriptive statistics)
- 몇 개의 의미있는 수치로 자료를 요약
- 중심위치측도 : 주어진 자료들이 어떤 값을 중심으로 분포되어 있는가 : 평균, 중앙값 등
- 산포도 : 자료들이 흩어져 있는 정도 : 분산, 표준편차 등
☑️ describe( )
Cholest = pd.read_csv('Cholest.csv')
Cholest.describe(include = 'all')

CholestMale = Cholest.loc[Cholest['Gender']=='Male']
CholestMale.describe()
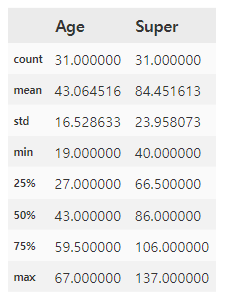
CholestFemale = Cholest.loc[Cholest.Gender == 'Female']
CholestFemale.describe()

• 양적 데이터 요약 02. 위치측도(Measure of location)
- 모집단을 표현하는 대표값을 중심으로 자료가 위치하므로 대표값을 위치측도(measure of location)라고도 함.
- 평균, 중앙값, 최빈값
☑️ 평균
## 평균(Mean : 산술평균)
## 가장 보편적이고 널리 사용되는 대표값.
## 관측치의 실제값을 사용함.
## 총합의 계산에 사용 가능함
## 양적자료에 의미가 있음
## 특이값(outlier)에 민감하게 영향을 받음.
## 비대칭적인 자료에 대해서는 평균을 사용하는 것이 바람직하지 않은 경우도 있음.
## sum(), mean()(pandas 패키지)
## trim_mean()(scipy패키지) : 절사평균, 특이값의 영향력을 없애기 위함
## 0.1 : 자료의 양극단에서 5%씩, 모두 10% 절사한 후 평균 계산
## sum, mean함수 (pandas 패키지), trim_mean함수(scipy패키지)
print(CholestFemale.Super.sum())
print()
print(CholestFemale.Super.mean())
print()
from scipy import stats
print(stats.trim_mean(CholestFemale.Super,0.1))# 합계
2567
# 평균
88.51724137931035
# 절사평균
87.68
☑️ 중앙값
## 중앙값(Median)
## 전체 주어진 관측치를 크기 순으로 나열했을 때 중앙에 위치하는 관측값
## 데이터의 순위에 관한 정보만을 이용함
## 특이값(outlier)에 영향을 덜 받는다. (robust)
## 데이터의 개수에 의한 영향을 받음
## 8, 4, 9, 1, 3 → 1, 3, 4, 8, 9 → 중앙값 = 4
## 8, 4, 1, 9 , 1, 3 → 1, 1, 3, 4, 8, 9 → 중앙값 = (3+4)/2 = 3.5
print(CholestFemale.Super.min())
print()
print(CholestFemale.Super.median())
print()
print(CholestFemale.Super.max())# 최소값
35
# 중앙값
84.0
# 최대값
146
☑️최빈값
## 최빈값(Mode)
## 전체 주어진 관측치들 중에서 가장 빈도가 높은 값
## 명목척도로 측정된 자료에 대한 대표값으로 주로 사용됨
## 예. 4, 5, 5, 6, 6, 6, 8, 9 → 최빈값 = 6
☑️정렬
## 정렬
## DATA.sort_values(by=["Super"]) : 과포화율 값을 기준으로 오름차순 정렬(pandas 패키지)
CholestFemale.sort_values(by = ['Super'])

• 양적 데이터 요약 03. 산포도(Measure of Dispersion)
- 데이터가 퍼져 있는 정도
- 분산, 표준편차, 변동계수, 표준화, 분위수, 범위, 사분위수 범위, 왜도, 첨도
☑️ 분산(variance)
## 분산(variance)
## 편차(평균과의 차이)의 제곱합을 자유도 n-1로 나눈 것
## 분산 직접 구하는 법
s2 = ((CholestFemale.Super - CholestFemale.Super.mean())**2).sum()
n = len(CholestFemale.Super)
print(s2/(n-1))
print()
## 분산 - var()
print(CholestFemale.Super.var())
print()760.9014778325125
760.9014778325125
☑️ 표준편차(Standard Deviation)
## 관측치들의 측정단위와 표준편차의 측정단위는 같음
## 표준편차가 작을수록 자료가 평균에 근접해서 분포함
## 표준편차가 0이면 자료의 관측치의 퍼짐이 전혀 없이 모두 같은 값을 지님.
## 표준편차 - std()
print(CholestFemale.Super.std())
☑️ 변동계수(coefficient of variation; 변이계수)
## 변동계수(coefficient of variation; 변이계수)
## 자료의 측정단위에 의존하지 않는 상대적인 산포의 측도
## 측정단위가 다르거나 평균에 큰 차이가 있는 자료들의 산포를 비교할 때 사용
## 0에 가까울수록 평균에 가까이 있음을 의미함
## 이를 구해주는 함수가 없기 때문에, 식을 기억하고 있기!!
## 변동계수(%) = (표준편차 / 평균) * 100
## ≪예≫ 키와 몸무게
## 원래는 두 개의 단위가 달라 비교가 어렵지만, 변동계수로 데이터의 분포를 비교할 수 있음
## 몸무게 : 72 74 68 76 74 69 72 79 70 69 77 73
## 키 : 180 168 225 201 189 192 197 162 174 171 185 210
## 몸무게 → 평균 : 72.75 표준편차 : 3.44 변동계수 : 4.73(%)
## 키 → 평균 : 187.83 표준편차 : 18.47 변동계수 : 9.83(%)
100*CholestFemale.Super.std()/CholestFemale.Super.mean()31.162790714831438
☑️ 표준화(standardization)
## 관측치의 상대적 위치의 척도로 사용됨.
## 관측치간 상대적인 크기를 비교할 수 있음.
## 관측치 전체 데이터 내에서의 위치를 나타내는 데 효율적으로 사용됨.
## 표준점수가 ∓2.0(또는 ∓3.0)을 벗어나면 특이값으로 볼 수 있음.
## 중심화 (centering)
## 평균이 0이 되도록 함.
## 중심으로부터의 편차에 관심을 가짐.
## 척도화 (scaling)
## 표준편차가 1이 되도록 함.
## 측정단위 자체를 없앰.
☑️ 분위수(Quantile)
## 백분위수(percentile)
## c백분위수는 전체 관측치들의 c%가 그 값 아래에 있고 나머지는 그 값 위에 있다는것을 의미함
## 사분위수(quartile)
## 예) 10, 15, 17, 25, 32, 40, 47, 51, 55, 63, 72
## 25백분위수 = 17 = Q1(제1사분위수)
## 50백분위수 = 40 = Q2(제2사분위수) = 중앙값
## 75백분위수 = 55 = Q3(제3사분위수)
## 이를 통해 BOX plot을 그릴 수 있음
## Interquartile range = Q3 - Q1
## quantile()(pandas 패키지) : 사분위수 계산
print(CholestFemale.Super.quantile([0.25,0.5,0.75]))0.25 73.0
0.50 84.0
0.75 107.0
Name: Super, dtype: float64
☑️ 범위(Range)
## 범위 : 최대 - 최소
## 이상치의 영향을 많이 받음 (= 평균, 표준편차)
## 두 가지 방법 사용 가능
## np.ptp()(numpy패키지) : 범위 계산
## quantile([0,1]).diff()(pandas 패키지)
import numpy as np
print(np.ptp(CholestFemale.Super))
print()
print(CholestFemale.Super.max() - CholestFemale.Super.min())
print()
print(CholestFemale.Super.quantile([0,1]).diff())#1
111
#2
111
#3
0.0 NaN
1.0 111.0
Name: Super, dtype: float64
☑️ 사분위수 범위(Interquantile Range)
## 사분위수 범위
## iqr()(scipy패키지) : 사분위수 범위 계산
## 이상치의 영향을 덜 받음
print(CholestFemale.Super.quantile(0.75) - CholestFemale.Super.quantile(0.25))
print()
from scipy.stats import iqr
print(iqr(CholestFemale.Super))#1
34.0
#2
34.0
☑️ 왜도
## 왜도(Skewness)
## 비대칭(asymmetry) 정도
## 대칭이면 정규분포
## left or negative skew (negative value)
## right or positive skew (positive value)
print(CholestFemale.Super.skew())
print()0.4549746453237919
☑️ 첨도
## 첨도(Kurtosis)
## 뾰족한(peakedness) 정도
## <0 : flat (left distribution)
## =0 : a normal Distribution
## >0 : steep (right distribution).
print(CholestFemale.Super.kurt())
print()-0.30781595830335196
• 양적 데이터 요약 04. 그래프
- 히스토그램, 상자그림, 줄기-잎 그림
☑️ 히스토그램(Histogram)
## 양적(수치형)데이터에 대하여 적절한 구간으로 나누어
## 빈도와 퍼센트를 계산하고 이를 막대그래프의 형태로 표현
## 자료의 분포를 시각적으로 이해 가능
## plt.hist()
## DataFrame.hist(column=None, by=None, …)
## bins 옵션 -> 계급의 수
CholestFemale.Age.hist(range=(10,80),bins=6,color="gray")

CholestMale.Age.hist(range=(10,80),bins=6,color="green")

Cholest.hist("Age", by = 'Gender')
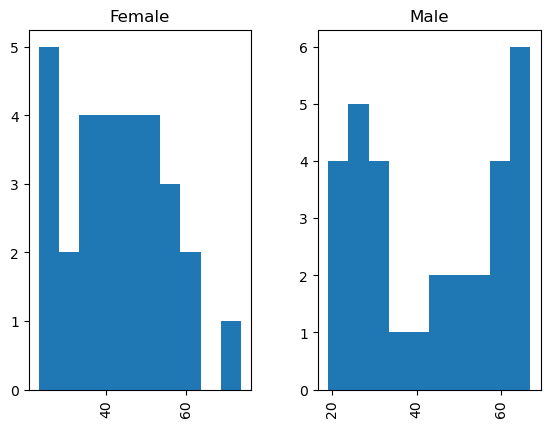
plt.hist(CholestMale.Age)

## plt 함수의 경우 density 옵션을 통해 y축을 확률밀도로 변경 가능
plt.hist(CholestFemale.Age, density = True)

☑️ 상자그림(Box Plot)
## 최소값, 제1사분위수, 제2사분위수(중앙값), 제3사분위수, 최대값
## 자료의 산포도 및 대칭성의 정도를 눈으로 쉽게 파악할 수 있음
## boxplot()(pandas패키지)(matplotlib패키지)
## plt.boxplot()
## DataFrame.boxplot(column=None, by=None, …) : 데이터프레임의 열(변수)에 대하여 상자그림 출력
## 이상치, 최대값, 최소값, 인접값
plt.boxplot(Cholest.Age)

## 남녀별 연령 상자그림
Cholest.boxplot("Age",by="Gender")
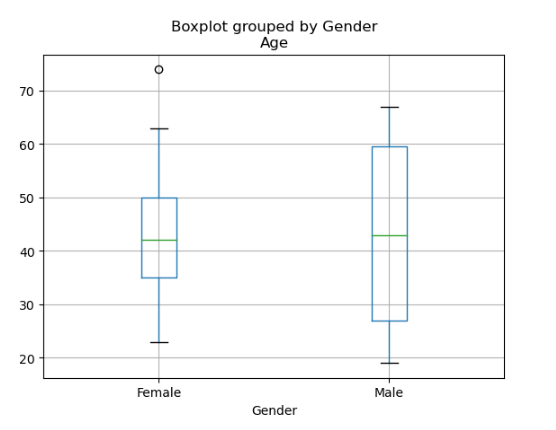
☑️ 줄기-잎 그림
## 전체 자료를 display하는 그래프
## 줄기(stem) 부분에 일부 정보 제시, 잎(leaf) 부분에 나머지의 정보 제공
## stem-graphic()(stemgraphic 패키지)
## stem-graphic(df, …) : 데이터프레임의 변수에 대하여 줄기-잎 그림 작성
import stemgraphic
# Stem-and Leaf Plot
stemgraphic.stem_graphic(CholestFemale.Age)
