모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

🎲 두 모집단에 대한 비교
실제 현실에 적용되는 경우는 대부분 두개 이상의 모집단의 특성을 비교함
• 두 모집단에 대한 비교의 예
- 새로운 약품을 개발하였을때 새로운 약품의 효능을 임상실험을 통하여 검증
- 새로운 약품을 사용한 환자와 사용하지 않은 환자간의 데이터를 비교하여 새로운 약품의 효능 비교
- 휴대폰의 사용시간이 성별(남, 여)에 따라 차이가 있는가를 검토하여 새로운 마케팅 제안
- 사회현상에 대한 남녀별 인식정도의 차이
- 흡연 집단과 비흡연 집단 간의 폐암 발생률의 차이
- 두 회사 제품에 대한 소비자들의 선호도 차이
주로 두 모집단의 모평균, 모비율, 모분산의 차이에 대한 가설검정 문제를 다룸
🎲 01. 모분산의 동일성에 대한 검정 : Bartlett, Levene 검정
고도의 정밀도를 요구하는 경우에는 정밀도에 대한 측도를 나타내는 분산에 대한 비교가 중요함. 예를 들어, 일정한 규격의 베어링을 생산하는 경우 각 제조공정에 따라 베어링의 평균 지름은 같으나 분산이 다르면 심각한 문제가 발생할 수 있음. 이러한 경우, 모분산을 비교함으로써 각 제조 공정에 따른 정밀도를 검증할 수 있음. 이에, 두 모집단의 평균 차이를 검정하는 과정에서 두 모분산의 동일성 ( $𝐻_0 ∶ 𝜎^2_1 = 𝜎^2_2$ ) 에 대한 검정을 수행해야 할 필요가 있음. 하지만 모분산은 모르기 때문에, 표본분산의 비를 사용해서 F검정을 수행.
• F-분포 : 두 정규모집단의 분산비에 대한 추론에 주로 사용됨
• rs : 랜덤표본 (확률표본)
- 랜덤표본의 특성 : 서로 동일한 모집단 분포를 가짐, 서로 독립 -> IID
- 비복원추출 -> 각 시행이 독립이 아님 & 모집단의 분포가 바뀜
- 복원추출 -> 각 시행이 서로 독립. 동일한 모집단의 분포. -> IID
- 유한모집단의 경우 -> 랜덤표본 : 비복원추출 -> 단, 표본 크기가 아주 큰 유한모집단이라고 생각하면 됨
- 무한모집단의 경우 -> 랜덤표본 : 복원추출
표본분포 : 모집단 $X$ ~ $N(μ, 𝜎^2)$ 에 대해 표본의 개수가 30개 이상이면 표본평균 $\bar{X}$ ~ $N(μ, 𝜎^2/n)$ 을 따름. 즉, 표본평균의 기댓값이 모평균과 같아짐. 이러한 성질을 불편성이라고 함. 또한, 표본평균의 분산은 $𝜎^2/n$ 을 따름.만약 모집단의 분포가 정규분포가 아니더라도 n의 크기가 충분히 크면 중심극한정리에 의해 정규분포라고 생각해도 무방함.
☑️ 모분산의 동일성에 대한 검정
• Bartlett 검정, Levene 검정 : 정규분포의 가정에 덜 민감함. 집단간 분산이 같은지 다른지 여부를 알아볼 때 사용하기도 하고 독립 2표본 t-검정 또는 일원분산분석(one-way ANOVA) 실시 전에 가정 때문에 확인하는 용도로 사용함. 또한 Bartlett 검정은 두 집단 뿐만 아니라 세 집단 이상에서도 사용할 수 있으며 이러한 경우 표본이 정규성을 보일때만 사용할 수 있음. 다만, Bartlett 검정보다는 Levene 검정이 정규분포의 가정에 훨씬 덜 민감함.
## 데이터 전처리
Reading = pd.read_csv("Reading.csv")
New = Reading[Reading.Group == 'New']
Old = Reading[Reading.Group=="Old"]
## 가설검정 1
from scipy import stats
stats.bartlett(New.Score,Old.Score) # Bartlett 검정. 귀무가설 기각 못함
## 가설검정 2
stats.levene(New.Score,Old.Score) # Levene 검정. 귀무가설 기각 못함
# 유의확률이 0.05보다 크기 때문에 유의수준 5%하에서 귀무가설을 기각할 수 없다.
# 즉, 두 방식에 의한 독해력 성적의 모분산은 같다고 할 수 있다.# Bartlett
BartlettResult(statistic=0.030098911091236386, pvalue=0.8622659908256447)
# Levene
LeveneResult(statistic=0.1978798586572438, pvalue=0.6632376240724351)
🎲 02. 독립표본에 의한 두 모평균의 비교 : 독립표본 T −검정
- 남학생과 여학생의 학업성취능력에 대한 평균이 같은가?
- 서로 다른 두 공장에서 생산된 냉장고에 있어 냉각능력의 평균은 같은가?
- 새로운 치료법과 기존의 치료법의 치료효과의 평균은 같은가?
• 모분산을 알고 있는 경우에는 표준정규분포를 그대로 사용
• 모분산을 모르지만 표본이 충분히 큰 경우에는 $σ$ 대신 표본분산 $s$ 와 표준정규분포를 사용해서 검정
• 모분산을 모르고 표본의 수가 적은 경우에는, $s$ 와 t-분포를 사용해서 추정
- 등분산가정 : 두 모분산 시그마가 같다고 두고, 공통분산을 만들어 T 분포에 대해 가설 검정을 수행.
- 이분산가정 : 두 모분산이 다른가에 대해 가설검정
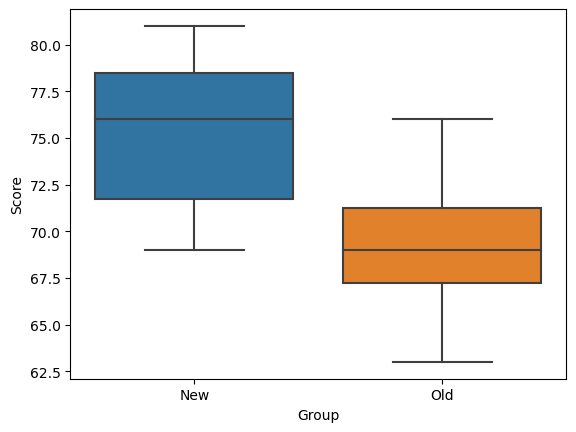
☑️ 시각화를 통한 데이터 분포 및 평균 비교
import seaborn as sns
sns.boxplot(x='Group',y='Score',data=Reading) # 상자그림
## 전반적인 분포도 보여주는 viloin plot
sns.violinplot(x='Group',y='Score',data=Reading) # 바이올린 플롯

☑️ 등분산가정 : ttest_ind(a, b, equal_var=True, alternative) - equal_var = False 면 이분산가정
# 양측검정
from scipy.stats import ttest_ind
print(ttest_ind(New.Score,Old.Score,equal_var = True))
## 검정 결과 p-value가 0.05보다 작기 때문에 귀무가설 기각.
## 즉, 새로운 학습방법에 따라 두 집단의 평균 성적이 달라짐.>> Ttest_indResult(statistic=2.9536127902039953, pvalue=0.010470744188033123)
☑️ 이분산가정 : ttest_ind(a, b, alternative, usevar="unequal") - usevar = 'pooled' 면 등분산가정
# 단측검정
## scipy.stats 모델에서는 equal_var = False, alternative = 'greater' 로 진행
from statsmodels.stats.weightstats import ttest_ind
ttest_ind(New.Score,Old.Score, alternative="larger", usevar="unequal")
## 검정 결과 p-value가 0.05보다 작기 때문에 귀무가설 기각.
## 즉, 새로운 학습방법을 적용한 집단의 평균 성적이 더 높다고 할 수 있음.>> (2.9536127902039953, 0.005256688626975243, 13.935945095796395)
🎲 03. 독립표본에 의한 두 모비율의 비교 : 이항분포, 정규근사
성인 남녀의 흡연율, 서로 다른 두 제조 공정에서의 불량률의 비교 등과 같이 두 모집단의 모비율 차에 대한 추론
두가지 특성값만 가지는 두 모집단에서 랜덤표본을 서로 독립적으로 추출하여 두 모비율 $𝒑𝟏$, $𝒑𝟐$ 를 비교
$𝑋_1$ ~ $𝐵(𝑛_1, 𝑝_1)$, $𝑋_2$ ~ $𝐵(𝑛_2, 𝑝_2)$ 인 이항분포를 따르며, 서로 독립.
• 1. 피셔의 정확검정(Fisher’s exact test) : 표본의 크기가 크지 않은 경우 & $𝑋_1$과 $𝑋_2$가 이항분포를 따를 때 두 모비율의 차이에 대한 검정. 즉, $𝑋_1$ ~ $𝐵(𝑛_1, 𝑝_1)$ , $𝑋_2$ ~ $𝐵(𝑛_2, 𝑝_2)$ 를 따르고 서로 독립일 때 두 모비율의 차이에 대한 검정 수행.
• 2. 정규근사 검정 : 표본의 크기가 충분히 큰 경우 & 두 모비율의 차이 $𝒑_𝟏$ − $𝒑_𝟐$ 의 추정량에 대한 구간 추정. 즉 $𝑋_1$ ~ $𝐵(𝑛_1, 𝑝_1)$, $𝑋_2$ ~ $𝐵(𝑛_2, 𝑝_2)$ 를 따르고 서로 독립일 때, 표본크기 $𝒏_𝟏$, $𝒏_𝟐$ 가 충분히 크면 이항분포의 정규근사에 의해 $𝑋_1$ ≈ $𝑁(𝑛_1𝑝_1, 𝑛_1𝑝_1(1 − 𝑝_1))$, $𝑋_2$ ≈ $𝑁(𝑛_2𝑝_2, 𝑛_2𝑝_2(1 − 𝑝_2))$ 를 따름. 두 분포에서의 모비율의 차이에 대한 검정 수행.
상황 : 현 정부에 대한 지지율이 성인 남녀별로 차이가 있는가를 알아보기 위해 조사를 해 본 결과, 임의로 뽑은 250명 성인 남자 중 110명이 현 정부를 지지하였고, 200명의 성인 여자 중 104명이 현 정부를 지지하는 것으로 나타났다. 성인 남녀별로 현 정부에 대한 지지율에 차이가 있는지 유의수준 5%하에서 검정하자.
☑️ 두 모비율의 검정을 위해서는 데이터를 분할표 형태로 변환해야 함 : pd.crosstab(index, columns)
# 데이터 전처리 - 분할표 작성
Support = pd.read_csv('Support.csv')
SupportTable = pd.crosstab(index=Support["Gender"], columns=Support["YesNo"])
SupportTable

☑️ 01. 피셔의 정확검정
## 피셔의 정확검정 수행, 오즈비와 유의확률 출력
## 유의확률 𝑝 − 𝑣𝑎𝑙𝑢𝑒 = 0.1063 > 𝛼 = 0.05 이므로 유의수준 5%하에서 귀무가설을 기각할 수 없다.
## 즉, 정부에 대한 지지율이 남녀별로 차이가 있다고 할 수 없다.
from scipy.stats import fisher_exact
fisher_exact(SupportTable,alternative='two-sided')>> (0.7252747252747253, 0.10634531219760412)
☑️ 02. 정규근사 검정
## 분할표에 대하여 카이제곱 통계량을 이용한 독립성 검정 수행
## 유의확률 𝑝 − 𝑣𝑎𝑙𝑢𝑒 = 0.1110 > 𝛼 = 0.05 이므로 유의수준 5%하에서 귀무가설을 기각할 수 없다.
## 즉, 정부에 대한 지지율이 남녀별로 차이가 있다고 할 수 없다.
from scipy.stats import chi2_contingency
chi2_contingency(SupportTable)# 검정통계량, p-value, 자유도, 기댓값 출력
(2.5395141968952935,
0.1110289428837834,
1,
array([[104.88888889, 95.11111111],
[131.11111111, 118.88888889]]))
🎲 04. 대응표본에 의한 두 모평균의 비교 : 대응표본 T−검정
두 모집단의 비교 실험에서 주의할 점 : 두 모집단의 실험단위들이 동질적이여야 함. 예를 들어 두 종류의 약품을 비교하고자 하는 경우, 실험단위들이 동질적이지 않으면 반응값의 차이가 순수한 처리효과에 의한 차이인지 혹은 성별, 연령별, 증상 등 실험에서 고려되지 않은 다른 요인에 의한 차이인지를 구별하기 어려움. 또한 두 종류의 운동화의 마모량을 비교하고자 하는 경우, 실험대상의 연령, 성, 보행습관 등에 의해 순수한 운동화의 품질차이를 알 수 없음. 즉, 실험에서 조절할 수 없는 요인(교락요인, confounding factor)으로 인해 순수한 실제 처리효과의 차이를 알기 어려움.
다만 성, 연령, 습관, 증상 등을 모두 동일한 개체들만으로 실험을 하는 것은 현실적으로 매우 어려움. 따라서 이와 같은 문제점을 해결하기 위해 대응표본(짝지은 표본)을 구성하여 실험을 수행함.
• 대응비교 (paired comparison)
실험단위를 동질적인 쌍으로 묶은 다음 각 쌍에 대하여 랜덤하게 두 처리를 적용하고, 각 쌍에서 얻어진 반응값의 차이를 이용하여 두 모평균을 비교하는 것
상황 : 학생15명에게 컴퓨터 교육을 실시하기 이전의 통계학 시험성적(Pretest)과 교육을 실시한 후의 성적(Posttest)을 얻은 것이다. 컴퓨터 교육을 실시한 후의 통계학 시험성적이 더 높다고 할 수 있는지 유의수준 5%하에서 검정하시오.
☑️ 대응표본 T검정 : ttest_rel(a, b, alternative)
## 유의확률 𝑝 − 값 : 0.00397이므로 귀무가설을 기각할 수 있음.
## 즉 컴퓨터 교육을 실시한 후의 통계학 시험성적이 실시 전의 통계학 성적보다 높다고 할 수 있음.
from scipy.stats import ttest_rel
ttest_rel(Paired.Pretest, Paired.Posttest, alternative="less")>> Ttest_relResult(statistic=-3.093705670004429, pvalue=0.003965461614513267)