모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

🎲 상관분석 (correlation analysis)
데이터 분석 시 주요 관심 대상 중의 하나는 변수들간의 상호연관성을 분석하는 것.
이때, 상관분석은 변수들 간의 선형적인 상호 연관성을 알아보는 분석 기법임.
하지만 상관관계가 인과관계를 의미하지는 않음.
산점도를 통해서 두 변수 간의 상호연관성과 그 강도를 확인할 수 있음.
☑️ 산점도 01. plt.plot( ), plt.scatter( )
import pandas as pd
import matplotlib.pyplot as plt
Student = pd.read_csv("D://data//Student.csv")
plt.plot('Income', 'Expense', '*', color = 'red', data = Student)
## plt.scatter('Income','Expense', data=Student) # 산점도
plt.xlabel('Income')
plt.ylabel('Expense')
plt.show()
## 두 변수 간의 앙의 상관관계를 확인 가능함.

☑️ 산점도 02. sns.jointplot( )
## 산점도 작성 – jointplot 함수(seaborn 패키지)
## jointplot(x= ,y= ,data= ,kind= , color= )
## jointplot함수를 사용하면 회귀직선, 신뢰구간, 주변 히스토그램등이 추가된 산점도를 쉽게 얻을 수 있음
import seaborn as sns
sns.jointplot(x = 'Income', y = 'Expense', data = Student, kind = "reg") ## 회귀직선 출력

☑️ 산점도 03. sns.pairplot( )
## 산점도 행렬 작성 : pairplot 함수(seaborn 패키지)
## pairplot( )(seaborn 패키지) : 산점도 행렬 출력
import seaborn as sns
sns.pairplot(Student.iloc[:,1:4])
## PairGrid(data=, ) 데이터의 쌍별 관게를 그리기 위한 하부 plot의 격자를 출력.
## 원하는 그림을 위한 빈 격자 방을 만들어 줌
g = sns.PairGrid(Student.iloc[:,1:4])
g.map_upper(sns.scatterplot) # 대각선 위 : 산점도
g.map_lower(sns.kdeplot) # 대각선 아래 : Kernel Density
g.map_diag(sns.kdeplot,lw=3) # 대각선 : Kernel Density, 선 너비=3


🎲 상관계수 (correlation coefficient)
'연속형 변수'들 간의 연관성을 측정하는데 사용. 가구당 실질소득과 저축률, 섭취한 알코올의 양과 맥박수, 지능지수와 학업성적 등과 같이 '서로 관련이 있는' 두 변수에 대한 관찰값들이 쌍으로 주어졌을 때, 두 변수들 간의 관계를 나타냄.
일반적으로, 종속변수의 편차와 독립변수의 편차의 곱이 양수이면 두 변수는 같은 방향으로 움직임을 의미함. 반면 곱이 음수이면, 두 변수는 서로 다른 방향으로 움직임. 이와 비슷한 관계로, 공분산 개념이 존재함.
• 공분산 (-무한대 ~ 무한대)
- 두 변수 간의 공분산이 양수면 두 변수 사이에는 양의 관계가 있음
- 음수이면 두 변수 사이에는 음의 관계가 있음
- 하지만 공분산은 측정단위의 변화에 영향을 받기에, 실제로 얼마나 많은 관계를 가지고 있는지는 알려주지 않음
- 즉, 관계의 부호는 파악할 수 있지만 두 변수 간의 상호연관성의 정도는 알 수 없음
- 이를 보완하기 위해서, 상관계수를 사용함
• 상관계수 (Pearson’s Correlation Coefficient) : -1 ~ 1
- 모공분산의 추정량 : 표본공분산 $s_{xy}$
- 모상관계수 : $p_{xy} = Corr(X, Y) = \frac{Cov(X, Y)}{𝝈_x * 𝝈_y} = \frac{𝝈_{xy}}{𝝈_x * 𝝈_y}$
- 모상관계수의 추정량 : 표본상관계수 = $r_{xy} = \frac{s_{xy}}{s_x * s_y}$
즉, 상관계수는 공분산을 두 변수의 표준편차의 곱으로 나눔으로써 표준화된 두 변수의 공분산이라 할 수 있음.
- 𝐶𝑜𝑟𝑟 (𝑋, 𝑌)→ 1 : 강한 양의 상관관계
- 𝐶𝑜𝑟𝑟 (𝑋, 𝑌)→ −1 : 강한 음의 상관관계
- 𝐶𝑜𝑟𝑟 (𝑋, 𝑌)→ 0 : 선형의 관계가 없음
공분산과 달리 관계의 부호와 두 변수 간의 상호연관성의 강도도 보여줌
- 상관계수의 부호는 증감의 방향성을 나타냄
- 상관계수의 절대값의 크기는 직선의 주변에 자료가 어느 정도 집중되어 있는지를 나타냄
- 상관계수의 절댓값이 커질수록 자료가 집중되어 분포됨을 의미함
단, 상관계수는 두 변수의 ‘선형집중성’만을 재는 척도로서 비선형 연관관계를 반영하지 못함
• 상관계수를 통한 두 변수 간 상관분석
- 상관계수의 추정과 검정
- 표본상관계수 : 피어슨(Pearson) 의 적률상관계수
- 표본상관계수 $r_{xy} = \frac{s_{xy}}{s_x * s_y}$
- 표본상관계수를 이용하여 모상관계수 $𝝆$ 에 대한 검정
- 두 확률변수의 모집단의 분포가 이변량 정규분포임을 가정
- 가설 $𝑯_𝟎$ : $𝝆 = 𝟎$ $𝒗𝒔$ $𝑯_1$ : $𝝆 ≠ 𝟎$ $(𝝆 > 𝟎, 𝝆 < 𝟎)$
- 스피어만(Spearman)의 순위상관계수
- 두 확률변수의 모집단의 분포가 이변량 정규분포로부터 벗어나 있거나 데이터에 특이값이 존재할 때 사용
- 비모수적 방법에 의한 상관계수
- 두 변수 $𝑿$와 $𝒀$에 대한 $𝒏$개의 데이터 $(𝒙_𝒊, 𝒚_𝒊)$를 각 변수별로 순위화하여 얻은 값
- 이 때 스피어만(Spearman)의 순위상관계수(rank correlation coefficient)는 두 변수의 순위만을 이용하여 계산
- $𝒅_𝒊$ = $𝑸_𝒊$ − $𝑹_𝒊$ : $𝒊$ 번째 데이터 값에서의 순위차이를 의미함
- 순위데이터의 일치쌍과 불일치쌍의 개념을 이용한 켄달의 타우($𝝉$) 등도 비모수적인 상관계수로서 사용함
☑️ 상관계수의 계산 : DataFrame.corr(method, min_periods)
## method
## “pearson”(피어슨의 상관계수)
## “Kendal”(켄달의 타우)
## “spearman”(스피어만의 순위상관계수) 지정
## 기본값은 method=“pearson”
## min_periods= : 유효한 결과를 얻기 위한 변수들의 짝별 최소 관측치 수를 지정. 기본값은 min_periods=1.
#import pandas as pd
Student.iloc[:,1:4].corr(method='pearson') # 상관계수의 계산
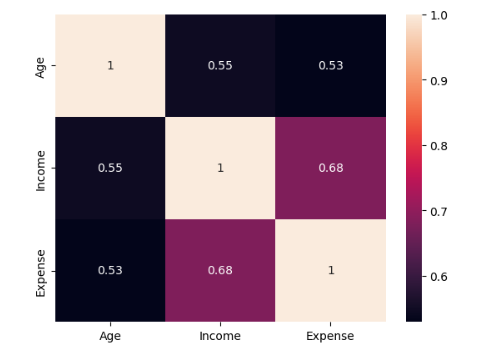
## 모든 변수들간의 상관계수가 0.5이상으로 변수들간의 상관관계가 비교적으로 높다는 것을 알 수 있음.
☑️ 상관계수 검정 : pearsonr(x, y) - 두 변수 간 피어슨 상관계수 및 무상관 귀무가설에 대한 p-값 출력.
from scipy.stats import pearsonr
pearsonr(Student.Income, Student.Expense)
## 상관계수, p-value
## 유의수준 5%하에서 귀무가설을 기각한다.
## 즉, 두 변수 Income과 Expense간의 모상관계수가 0이 아니라고 할 수 있다>> (0.6812956535794541, 0.0026006496946941998)
☑️ 상관계수 검정 : DataFrame.pairwise_corr(tail, method) - 상관계수에 대한 유의확률 및 신뢰구간 등의 통계량 제시
## 상관분석 : 상관계수와 𝒑-값 함께 출력하기
## DataFrame.pairwise_corr(tail= ,method= )(pingouin패키지)
## 데이터 프레임의 변수들에 대한 상관계수 출력.
## Corr함수와 기능이 유사하나, 상관계수에 대한 유의확률 및 신뢰구간 등의 다양한 통계량 제시.
## tail= : 상관계수 검정을 위한 p-값 출력시 “one-sided”(단측검정) 또는 “two-sided”(양측검정)을 지정
import pingouin as pg
Student.iloc[:, 1:4].pairwise_corr(method = 'pearson').round(3)

☑️ 상관계수의 그래프 표현 : sns.heatmap(corrMatrix, annot)
## heatmap(data=, vmin=, vmax=)(seaborn패키지) : 다양한 색으로 표현된 시각의 히트맵 행렬 출력
## 상관계수행렬
corrMatrix = Student.iloc[:, 1:4].corr(method = 'pearson')
sns.heatmap(corrMatrix, annot = True)
plt.show()
🎲 편상관계수
• 의사 상관(Pseudo Correlation)
- 실제적인 연관관계가 없음에도 불구하고 상관계수가 크게 나타나는 경우
- 제 3의 변수에 의하여 상관관계가 나타나는 경우
- 혈압-월급 & 혈압-나이-월급 간의 관계
• 편상관계수(partial correlation coefficient)
- $𝜌(𝑥_1, 𝑥_2 | 𝑧_1, ⋯ , 𝑧_𝑝)$ : 통제변수들 $𝑧_1, ⋯ , 𝑧_𝑝$ 가 같은 값으로 통제되었을 경우 두 변수 $𝑥_1$ 과 $𝑥_2$ 사이의 상관계수
- 나이를 고정해두고, 혈압과 월급 간의 상관관계를 파악
- 두 변수가 통제변수와 공유하는 부분을 각각 제거한 후 두 변수 간의 순수한 연관성을 측정함
• 상황 : 특정 제품에 대하여 20명의 고객으로부터 연령, 기능 만족도, 디자인 만족도를 조사하여 얻은 데이터에서, 변수 Age(나이)를 통제하였을 때 Satis1(기능 만족도)과 Satis2(디자인 만족도)의 편상관계수를 구하고 그 의미를 해석하시오.
☑️ 01. 단순상관계수 계산
## 1. 단순상관계수 계산
Satis = pd.read_csv('D://data/Satis.csv')
Satis.iloc[:, 1:4].corr().round(3)
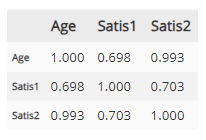
☑️ 02. 편상관계수 계산 : DataFrame.pcorr( )
## 2. 편상관계수 계산
## DataFrame.partial_corr(x=, y=, covar=, tail=, method=)(pingouin패키지)
## 변수 간의 편상관계수 출력
import pingouin as pg
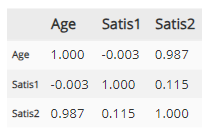
Satis.iloc[:, 1:4].pcorr().round(3)
## r(Age, Satis1 | Satis2) = -0.003
## r(Age, Satis2 | Satis1) = 0.987
## r(Satis1, Satis2 | Age) = 0.115
## 변수 Age를 통제했을 때 Satis1, Satis2의 편상관계수를 구하면 r(Satis1, Satis2 | Age) = 0.115
## 즉, 두 변수의 단순상관계수 0.703보댜 작음
☑️ 03. 두 변수 간 편상관계수 계산 : DataFrame.partial_corr(x, y, covar, tail, method)
Satis.partial_corr(x = 'Satis1', y = 'Satis2', covar = 'Age').round(3)
## 두 변수 간의 편상관계수는 0.115
## 두 변수 간의 모상관계수가 0이 아니라는 대립가설에 대해서
## p-value가 0.639 이므로 유의수준 5% 하에서 유의하지 않다
## 따라서, 통제변수 Age가 같은 값을 가지도록 고정한다면 Satis1, Satis2 간의 연관성이 크지 않음.
## 나이가 클수록 기능만족도와 디자인만족도가 모두 커지는 경향이 있으며(Age가 매개변수 역할)
## 나이가 같도록 통제하면(같은 나이를 가진 사람들만 조사) 두 만족도 사이에는 연관성이 작음
☑️ 산점도를 통한 편상관계수 검증 : sns.jointplot(x, y, data, hue)
## 연령대별(20대, 30대)로 변수 Satis1과 Satis2에 대한 산점도를 작성
import seaborn as sns
sns.jointplot(x = 'Satis1', y = 'Satis2', data = Satis, hue = 'AgeGroup')
## 연령대별로 구분할 경우, 두 변수의 상관성이 상당히 낮아짐

☑️ 데이터 세그먼테이션을 통한 편상관계수 검증
## 연령대별(20대, 30대)로 변수 Satis1(기능만족도)와 Satis2(디자인만족도)에 대한 상관계수 계산
SatisUnder30 = Satis.loc[Satis.AgeGroup == 'Under30']
SatisOver30 = Satis.loc[Satis.AgeGroup == 'Over30']
from scipy.stats import pearsonr
print(pearsonr(SatisUnder30.Satis1, SatisUnder30.Satis2))
print(pearsonr(SatisOver30.Satis1, SatisOver30.Satis2))
## 각 연령대에서 Satis1(기능만족도)와 Satis2(디자인만족도)의 상관계수가 매우 작고
## 유의확률(p-value)도 각각 0.390과 0.575로서 유의수준 5%하에서 유의하지 않음을 알 수 있음>> (0.38797014489949266, 0.38979066100658993)
>> (0.20330375111582555, 0.5262489862356583)
🎲 측정도구의 신뢰도 분석
• 문항의 신뢰성 분석 : 사회조사에서 관념적이거나 개념을 수량화 하기 위하여 각 문항을 4점 척도 또는 5점 척도 등을 사용하여 질문을 작성하고 이들 문항의 점수의 합을 특정 개념에 대한 관측값으로 사용하는 경우가 많음. 이 경우, 각 문항들이 동일한 개념을 묻는 질문이 되도록 설문을 구성해야 함. 동일한 개념을 측정하기 위하여 사용된 문항들에 대한 측정의 신뢰도(reliability)가 주요 관심대상이 되며, 문항들의 신뢰도가 높으면 문항 점수들의 합계(평균)을 특정 개념에 대한 지표로 사용할 수 있음.
• 리커트 척도(Likert scales) : 예를 들어 현 정부의 금융정책에 대한 지지도를 측정하기 위해 여러 문항을 만들고, 각 문항에 대해서 ‘대단히 반대한다’, ‘반대한다’, ‘잘모르겠다’, ‘찬성한다’, ‘대단히 찬성한다‘ 와 같은 응답을 1~5점으로 환산해 수량화 진행. 만약 지지도를 측정하는 문항이 10개 있다면, 이들의 점수의 합을 지지도에 대한 관측값으로 간주함. 이 때 10개의 문항들이 모두 같은 개념을 묻는 문항들이면 신뢰성(reliability)이 높다고 하고, 각 문항들의 개념이 불분명하면 문항의 신뢰성은 떨어짐.
• 크론바흐의 알파계수
- 5점 척도를 사용하는 $𝒏$개의 문항의 점수의 합을 $𝑿$라 하면, $𝑿$는 참값 $𝑻$ 와 오차항 $𝒆$ 의 합으로 표현
- $X$ = $T$ + $e$ (단 $T, e$ 는 독립)
- 이제 이 $𝑿$ 와 동일한 문항의 점수합 $𝑿’$이 있다면 $𝑿’$은 $𝑻$ + $𝒆′$ (단, $𝒆′$은 $T$ 및 $𝒆$ 와 독립)
- 만약 두 문항이 같은 종류에 대해 묻고 있다면, 두 점수의 합 $X$, $X'$ 간의 상관계수는 클 것임
- 왜냐하면, $𝑿$ 와 $𝑿’$의 상관계수는 등분산성과 등공분산성의 가정에 의해 같은 방향으로 나아갈 것이기 때문
- 이때 두 문항 간의 상관계수이자 신뢰도 𝝆를 추정하는 대표적 방법은 크론바흐의 알파($𝜶$)계수
- $0 ≤ 𝛼 ≤ 1$
- $𝛼$ 의 값이 1에 가까울수록 신뢰성이 높은 문항들임을 의미
- cronbach_alpha(data= ,ci= ) (pingouin패키지)
- 내적일관성 신뢰도 계산을 위한 크론바흐 알파값과 신뢰구간을 출력
• 상황 : 상사의 각 부분에 대한 능력을 평가하기 위한 설문 문항이 있다. 1,2,3 문항은 상사의 업무수행능력에 대한 평가를, 4,5,6,7 문항은 상사와의 공적 / 개인적 긴밀함에 대한 평가, 8,9,10 문항은 업무추진의 독자성을 평가하는 문항이다. 각각의 문항들이 평가목적에 올바르게 부합하는지 여부를 신뢰도분석을 통해 검정하시오.
☑️ ‘상사의 업무수행능력’에 대한 신뢰도 분석
## ‘상사의 업무수행능력’에 대한 신뢰도 분석
## Q01, Q02, Q03
## 문항별 상관계수
## 양의 상관관계
Ability = pd.read_csv('D://data/Ability.csv')
print(Ability[['Q01', 'Q02', 'Q03']].corr())
## 크론바흐 알파, 신뢰구간
import pingouin as pg
pg.cronbach_alpha(data = Ability[['Q01', 'Q02', 'Q03']])
## 크론바흐 알파계수의 값이 0.7352로서 내적일관성 신뢰도가 높다는 것을 알 수 있음## 상관계수
Q01 Q02 Q03
Q01 1.000000 0.596712 0.407001
Q02 0.596712 1.000000 0.433838
Q03 0.407001 0.433838 1.000000
## 크론바흐 알파 계수
(0.7351921832148215, array([0.697, 0.769]))
☑️ ‘상사와의 공적/개인적 긴밀함’에 대한 신뢰도 분석
## ‘상사와의 공적/개인적 긴밀함’에 대한 신뢰도 분석
## 'Q04', 'Q05', 'Q06', 'Q07'
## 문항별 상관계수
## 음의 상관관계 존재
print(Ability[['Q04', 'Q05', 'Q06', 'Q07']].corr())
## 크론바흐 알파, 신뢰구간
pg.cronbach_alpha(data = Ability[['Q04', 'Q05', 'Q06', 'Q07']])
## 크론바흐 알파계수의 값이 -0.222, 음수로 계산됨, 내적일관성의 신뢰도가 낮음.
## 즉, 방향성이 다른 문항이 존재한다는 의미
## 특히 Q7이 나머지 문항들의 점수와 음의 상관을 가짐
## 따라서, Q7은 다른 문항들과는 답변 순서를 반대로 정해야 할 필요가 있음.
## 관측값 {5, 4, 3, 2, 1}을 {1, 2, 3, 4, 5} 로 바꿔야 함.## 상관계수
Q04 Q05 Q06 Q07
Q04 1.000000 0.100787 0.307348 -0.351547
Q05 0.100787 1.000000 0.241432 -0.273088
Q06 0.307348 0.241432 1.000000 -0.350307
Q07 -0.351547 -0.273088 -0.350307 1.000000
## 크론바흐 알파 계수
(-0.2224494957901865, array([-0.386, -0.073]))
☑️ 데이터 전처리를 통한 문항 개선
## ‘상사와의 공적/개인적 긴밀함’에 대한 신뢰도 개선
Ability['Q07_R'] = 6 - Ability.Q07
## 문항별 상관계수
print(Ability[['Q04', 'Q05', 'Q06', 'Q07_R']].corr())
## 크론바흐 알파, 신뢰구간
pg.cronbach_alpha(data = Ability[['Q04', 'Q05', 'Q06', 'Q07_R']])
## Q7_R 관측값을 계산하여 새로운 변수를 생성하고 크론바흐 알파계수를 계산함.
## 0.5877로 내적일관성의 신도가 비교적 높게 나타남.
## 각 문항들과 다른 문항들의 점수와의 상관계수도 모두 양의 값을 가짐## 상관계수
Q04 Q05 Q06 Q07_R
Q04 1.000000 0.100787 0.307348 0.351547
Q05 0.100787 1.000000 0.241432 0.273088
Q06 0.307348 0.241432 1.000000 0.350307
Q07_R 0.351547 0.273088 0.350307 1.000000
## 크론바흐 알파 계수
(0.5876937990663734, array([0.532, 0.638]))
☑️ ‘업무추진의 독자성’에 대한 신뢰도 분석
## ‘업무추진의 독자성’에 대한 신뢰도 분석
## 'Q08', 'Q09', 'Q10'
## 문항별 상관계수
print(Ability[['Q08', 'Q09', 'Q10']].corr())
## 크론바흐 알파, 신뢰구간
pg.cronbach_alpha(data = Ability[['Q08', 'Q09', 'Q10']])
## 크론바흐 알파계수 값은 0.2511로 매우 낮게 나타남.
## Q8~Q10 문항들이 동일한 개념을 측정한다고 신뢰할 수 없음
## 하지만 양수이므로, 질문의 방향성이 다른 문항은 없음## 상관계수
Q08 Q09 Q10
Q08 1.000000 0.22047 0.067734
Q09 0.220470 1.00000 -0.001290
Q10 0.067734 -0.00129 1.000000
## 크론바흐 알파 계수
(0.25112573908813685, array([0.144, 0.347]))
☑️ 표준화 크론바흐 알파 계수 : 문항들의 척도가 동일하지 않은 경우에 사용
## 표준화 크론바흐 알파 계수
## 문항들의 척도가 동일하지 않은 경우에 사용
## 4점척도와 5점 척도를 함께 보는 경우 사용
import numpy as np
def CronbachAlpha(df):
df_corr = df.corr()
N = df.shape[1]
rs = np.array([])
for i, col in enumerate(df_corr.columns):
sum_ = df_corr[col][i+1:].values
rs = np.append(sum_, rs)
mean_r = np.mean(rs)
cronbach_alpha = (N * mean_r) / (1 + (N-1) * mean_r)
return cronbach_alpha
print(CronbachAlpha(Ability[['Q01', 'Q02', 'Q03']]))
print(CronbachAlpha(Ability[['Q04', 'Q05', 'Q06', 'Q07_R']]))
print(CronbachAlpha(Ability[['Q08', 'Q09', 'Q10']]))
## 표준화하지 않은 경우 크론바흐 알파와 비교
## 0.7352, 0.5877, 0.2511로 표준화했을때 크론바흐 알파계수와 거의 유사함.
## 문항들이 모두 5점 척도로 측정되었기 때문>> 0.7340559223240841
>> 0.5976014343918359
>> 0.24084556669287197