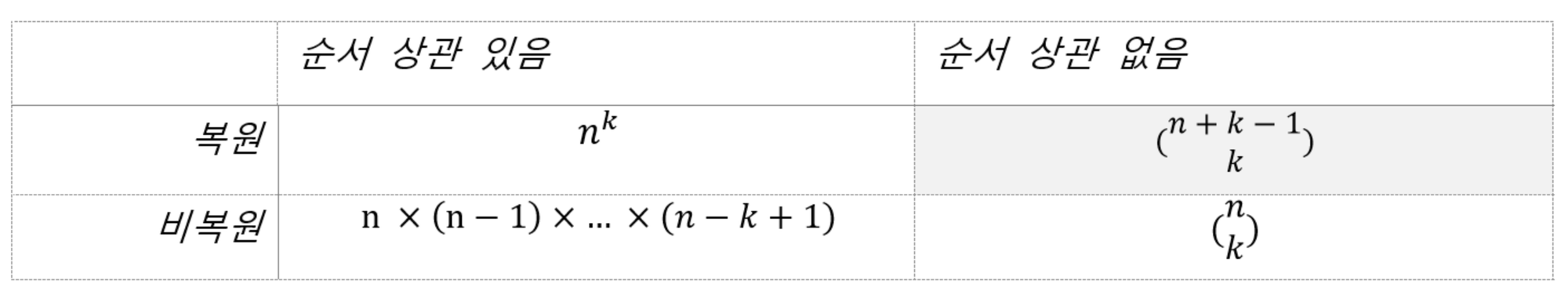👨‍💻 1강 - 확률과 셈 원리 (Probability and Counting)

 

모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!! 

 

 

---

 

오랜만에 글을 씁니다!! 

작년 11월 중순부터 서류 준비에, 면접 준비에 신경 쓰느라 공부한 내용을 정리할 여유가 없더라구요,,,

 

그치만 그 노력들이 결실을 맺어,

올해 1월 2일부터 IT 기업에서 Business Intelligence Analyst 로 근무중입니다 😀

(나중에 기회가 된다면, 취업기도 한번 써보겠습니다)

 

데이터 직군이다 보니 항상 무언가를 공부하고 배우는 중인데요, 

오늘부터는 저희 팀 내부에서 진행하는 스터디 내용을 정리하고자 합니다.

 

저희가 듣는 통계 강의는 HAVRD STATISTICS 110 이라는 강의인데요,

나온지 꽤 오래된 강의이긴 하지만 강의 목록을 보고 통계학의 가장 아랫단부터 설명해준다고 생각하여 선택하였습니다.

유튜브에서 무료로 보실 수 있으니 관심 있는 분은 보셔도 좋을 듯 합니다!!

 

Statistics 110: Probability

 

이번 포스팅은 그 첫 강의인  Probability and Counting, 즉 확률과 셈 원리에 대해 다루겠습니다.

 

---

 

학습목표

확률의 기초 용어(표본공간과 사건, 셈 원리)를 이해하고 적용한다.

 

키워드

• 표본공간
• 사건
• 셈 원리(곱의 법칙)
• 이항계수

 

 

---

내용정리

 

1. 확률

• 확률은 불확실성(uncertainty)을 계량화하는 것을 가능하게 해줌
  
  
  
• 확률을 수학적으로 접근할 수 있도록 해준 가장 큰 계기는 집합을 사용하는 아이디어
  • 이전에는 직관적인 관찰을 통해 추론을 바탕으로 문제를 해결하려 함 (heuristic) → 틀린 방식
    
    
  • 통계는 반직관적인 학문이다 → 열심히 찾고 공부할수록, 보다 직관적인 방향으로 문제 해결이 가능하다.
    
    
  • 즉, 사건에 대한 직관적인 아이디어를 연결하고 이를 수학적으로 정확하게 만드는 것이 확률의 의미이다.

 

• 표본공간(sample space)
  • 시행에서 발생 가능한 모든 경우의 집합
    
    
  • 일반적으로 S 라고 표현함
    
    
  • 주사위 두 개를 굴린다면 → 총 36가지의 경우로 구성된 표본공간이 생성됨
     

 

• 사건(event)
  • 표본공간의 부분집합
    
    

 

• 확률의 나이브한 정의
  
  • 사건 A가 발생할 확률.
    
    
  • $P(A) = \Large\frac{(사건 \ A가 \ 발생하는 \ 경우의 \ 수)}{(발생 \ 가능한 \ 모든 \ 경우의 \ 수)}$
    
    
  • 아래 두 가정이 명확한 경우만 가능.
    
    • 가정 1 : 모든 결과가 나올 확률이 동일하다는 가정
      
      
    • 가정 2 : 유한한 개수의 결과가 나온다는 가정 → 유한한 표본 공간 → 유한한 분모
      
      
    • i.e. 동일한 동전을 두번 던질 때 모두 뒷면이 나오는 확률 : 1 / 4

 

---

 

2. 셈 원리

• 확률의 정의에서, 분자와 분모를 계산하기 위한 원칙
  
  
• multiplication rule
  • 이전 시행과 독립적인 결과를 만드는 $r$ 개의 시행
    
    
  • 발생 가능한 경우의 수가 각각 $n_1,\ n_2,\ ...,\ n_r$ 가지인 $1,\ 2,\ ...,\ r$ 번의 시행에서
    
    
  • 발생 가능한 모든 경우의 수는 $n_1 \times n_2 \times ... \times n_r$
    
    
  • 트리 관점으로 생각할 것
    
    
    • i.e. 아이스크림
      • 콘 유형 : C, W
        
        
      • 맛 : 딸기, 바닐라, 초코
        
        
      • 총 6가지 경우의 수 존재   
        
        
        
    • i.e. 풀하우스 (동일숫자인 카드를 3장, 2장씩 보유하는 경우. 1이 3장, 9가 2장인 경우 등)
      • 가정 : 고루 섞인 카드 - 뽑을 확률 동일
        
        
      • 총 52장의 카드 중 5개의 카드를 받음
        
        
      • 가능한 총 경우의 수 : $_{52}C_5$
        
        
      • 풀하우스 경우의 수 : $13 \ ・ \ _4C_3 \ ・ \ 12 \ ・ \ _4C_2$
        
        
        
        
  • 이항계수(Binomail coeff)
    • 순서 상관없이, $n$개 중에서 $k$개를 추출하는 경우의 수
      
      
    • $_{n}C_k = \frac{n !}{(n-k)!k!}$
      
      
      
      
  • 표본추출(Sampling)
    • $n$개 중에서 $k$개를 추출하는 경우의 수
      
      
      

 

 

---