모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

🧩 저번 포스팅을 통해 object 간의 Distance Matrix를 만드는 법에 대해 알아보았습니다. 이제는 본격적으로 Distance measure에 대해 알아볼텐데, 이 measure들은 feature의 자료형에 따라 다르게 적용됩니다. 이번 포스팅에서는 categorical feature와 binary feature에 대한 measure에 대해 알아보도록 하겠습니다.
🚩 1. Nominal Categorical Attributes - 순서가 없는 범주형 데이터
🧩 Simple Matching
먼저 알아볼 방법은 simple matching 입니다. 이 방법을 통한 object 사이의 distance는 아래와 같이 구해집니다.
$$d(i,j)=(p−m)p$$
이때 m은 feature에 대해 같은 값의 개수이고, p는 feature의 개수를 의미합니다.
간단한 예를 한번 살펴봅시다.
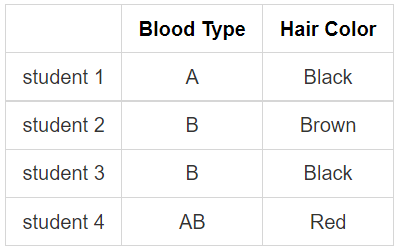
위에서 student 2와 3은 Blood Type은 같지만 Hair Color가 다르기 때문에 distance는 아래와 같습니다.
$$d(s2,s3)=\frac{(2-1)}{2}=\frac{1}{2}$$
반면 student 2와 student 4는 두 feature가 모두 다르기 때문에 distacne는 다음과 같습니다.
$$d(s2,s4)=\frac{(2-0)}{2}=1$$
이렇게 하면 간단하게 simple matching 을 통해 distance를 구할 수 있습니다.
🧩 Use a large number of binary attributes
각 nominal state에 대해 새로운 binary attribute를 생성하는 방법입니다.
즉, 범주형으로 주어진 각 feature들을 binary 형태로 바꿔주겠다는 의미입니다.
위 예시에 적용해 Blod type A를 0, B를 1로 바꾸고 Hair Color Black을 1, Brown을 0으로 바꿔 나타낼 수 있습니다.

그 후에 distance를 구하는 방법은 simple matching과 같습니다.
$$d(i,j)=\frac{(p-m)}{p}$$
🚩 2. Ordinal Categorical Attributes - 순서가 있는 범주형 데이터
🧩 위에서 다룬 nominal data와는 다르게 순위나 순서가 있는 자료형입니다.
이 데이터의 distance는 ordinal variables를 그것의 순위로 변경해 구할 수 있는데, 이는 아래와 같은 방식으로 정해집니다.
$$feature\;f,\;index\;\,i,\;\;r_{if}∈{1,2,...,M_{if}}\;\;and\;\;r_{if}=\;value\;ranking,\;M_{if}=\;amount$$
$$Z_{if}=\frac{r_{if}-1}{M_{if}-1}$$
수식만 보면 뭔가 복잡해보이지만 쉽게 생각하면 $M_{if}$는 전체 순위의 수를, $r_{if}$는 해당 변수의 순위를 나타냅니다.
예시를 한번 살펴보도록 합시다.
$$freshman = 1$$
$$sopomore = 2$$
$$junior = 3$$
$$senior = 4$$
에 대해서 각각의 Z값을 먼저 구해 보면,
$$Z_{if} = 0, \;\frac{1}{3}, \;\frac{2}{3},\;1$$ 로 계산됩니다.
Z값을 바탕으로 해서 distance를 구하게 되는데, 그 계산은 단순 뺼셈 연산을 사용하면 됩니다.
다만 distance가 음수일 수는 없기에, 큰값에서 작은 값을 빼준다고 생각하시면 됩니다.
$d(freshman,senior) = 1-0=1$
$d(junior,senior) = 1-\frac{2}{3}=\frac{1}{3}$
3. Binary Attributes - 이진변수
binary attribute들은 0또는 1의 값을 가지기 때문에, 이를 간단하게 합쳐서 하나의 table로 만들 수 있습니다.
이 table을 Contingency Table 이라 하는데, 그 모습은 아래와 같습니다.
📝 Contingency Table

두 object가 모두 1인 경우에는 $q$, 모두 0이면 $t$, (i,j) = (1,0) 이면 $s$, (0,1) 이면 $r$로 그 값이 집계됩니다.
contingency table 에서 distance를 구할때는 주로 s와 r을, similarity를 구할 때는 q와 t를 사용합니다.
⭐⭐ contingency table에 있어서 반드시 고려해야 할 점이 있습니다. 이는 저희가 binary로 나타내는 데이터는 두 가지 경우로 명확히 나눠져야 한다는 점입니다. 하지만 이러한 경우는 흔히 찾아보기가 힘들기 때문에, 이를 적극적으로 사용할 수 있는 도메인은 질병의 양성 / 음성을 판단하는 도메인입니다. 예를 들면 코로나 검사 결과가 양성(1)이냐 음성(0)이냐를 다루는 경우라 할 수 있습니다.
⭐⭐ 더욱 중요한 것은 질병 관련 조사에서 저희가 관심있는 대상은 대부분 양성인 경우입니다. 하지만 두 조사 대상이 모두 양성인 경우$(q)$보다는 당연히 음성$(t)$일 가능성이 높기에, 필연적으로 위의 contingency table에서 $q$보다 $t$가 월등히 큰 값을 가질 것입니다. 이렇게 asymmetric한 table에 대해서는 당연히 이 경우를 고려해야 주어야 합니다⭐⭐.
👉 이제 각각의 경우에 대한 distance를 구해보겠습니다.
🧩 Distance measure for symmetric binary variables
$$d(i,j)=\frac{r+s}{q+r+s+t}$$
🧩⭐Distance measure for asymmetric binary variables⭐
$$d(i,j)=\frac{r+s}{q+r+s}$$
🧩⭐Similarity measure for asymmetric binary variables⭐
$$Jaccard\;\,coefficient=Sim_{jaccard}(i,j)=\frac{q}{q+r+s}$$
예시를 한번 살펴보도록 합시다!!

어떤 질병에 관련된 7개의 feature를 가진 3개의 object로 구성된 데이터임을 확인할 수 있습니다. 이때 gender는 symmetric한 특징을 가지고 있기 때문에 이는 제외하고 distance를 계산해 줄 것입니다. 또한 test의 결과에서 나오는 P는 1로, N은 0으로 간주합니다. 이를 바탕으로 contingency table을 만들면 아래와 같습니다.
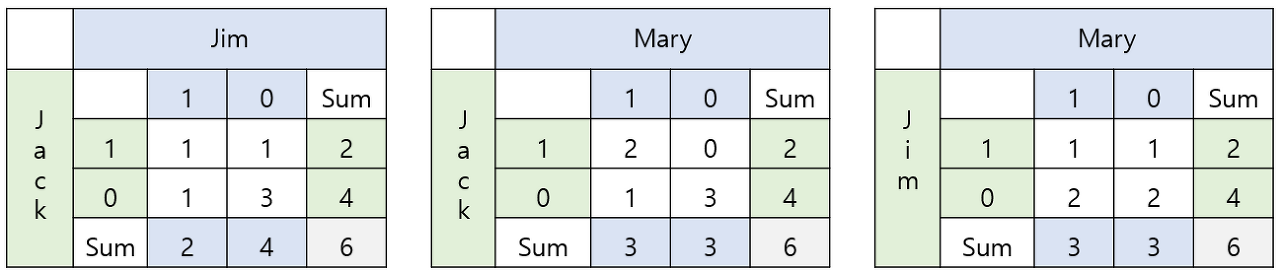
🧩 위의 공식에 따라서 distance를 구하겠습니다.
$$d(i,j)=\frac{r+s}{q+r+s}$$
$$d(jack,jim)=\frac{1+1}{1+1+1}=0.67$$
$$d(jack,mary)=\frac{0+1}{2+0+1}=0.33$$
$$d(jim,mary)=\frac{1+2}{1+1+2}=0.75$$
🧩 이렇게 해서 binary data에 대한 distance measure 역시 다뤄보았습니다. 고려해야 할 것도 있고, 그 경우마다 적용되는 공식도 살짝씩 달라지지만 서로 다른 것들로 distance를 계산하고 같은 것으로 similarity를 계산한다는 것만 기억하고 계시면 그렇게 어려운 개념은 아닐 것 같다고 생각합니다🙂.
🧩 이번 포스팅에서는 categorical data에 대한 distance measure를 알아보았습니다. 종류가 다양하고, 데이터의 도메인에 따라서 적용하는 법이 다르지만 위의 예시들만 잘 살펴봐도 나름 스근하게 넘어갈 수 있는 내용들인 것 같습니다😊. 앞으로 나올 내용들의 기초가 되는 부분들이기 때문에 나름 자세히 다뤄보았는데, 충분한 설명이 되었으면 좋겠네요. 이제 다음 포스팅에서는 Numerical Data의 distance를 구해보도록 하겠습니다🏃♂️🏃♂️.
💡위 포스팅은 한국외국어대학교 바이오메디컬공학부 고윤희 교수님의 [생명정보학을 위한 데이터마이닝] 강의를 바탕으로 합니다.
'📌 데이터마이닝 > 데이터 분포 확인' 카테고리의 다른 글
| 🚩 데이터마이닝 06. Document Frequency (0) | 2023.02.07 |
|---|---|
| 🚩 데이터마이닝 05. Numerical Distance (0) | 2023.02.07 |
| 🚩 데이터마이닝 03. Distance Matrix (2) | 2023.02.06 |
| 🚩 데이터마이닝 02. QQ Plot (0) | 2023.02.05 |
| 🚩 데이터마이닝 01. 소개 (0) | 2023.02.05 |