모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

🧩 개강 전에 며칠간 본가에 내려가 있다가 다시 올라와 글을 씁니다. 벌써 내일이면 개강인데, 시간이 참 빠르다는 생각이 드네요. 4학년이라 졸업프로젝트에 졸업논문으로 꽤나 바쁠 것 같다는 생각이 들지만, 가끔 와서 글을 쓸 수 있도록 하겠습니다.
🧩 이번 포스팅부터는 Dataset에서 Pattern을 찾는 Pattern Discovery 에 대해서 다룰 것입니다. 특히 이 부분은 생명정보학 분야에 있어서 꽤나 큰 비중을 차지하고, 데이터마이닝에 관련된 중요한 기법 역시 많이 나오기에 관심 있으신 분들은 주의깊게 보시면 좋을 것 같습니다 (당연히 양도 많습니다...😨😨). 이번 포스팅에서는 Pattern Discovery에 관련된 기초 개념부터 알아보도록 하겠습니다.
🚩 1. Pattern Doscovery 란??
▪ Patterns : 하나의 dataset에서 함께 발생하거나 연관관계가 깊은 것들.
- ex) 함께 팔린 물건들 / 같이 나타나는 단어들 / 함께 나타나는 sequence
▪ Pattern Doscovery : dataset에서 고유한 규칙을 찾는 것. 데이터마이닝의 기초 작업.
- Association / Correlation / Casuality analysis
- Mining Sequential / Structure Patterns
- 패턴분석 : 시공간 / 멀티미디어 / 시계열 / 스트림데이터
- Classification : pattern based analysis - Discriminative
- Cluster analysis : pattern based clustering - subspace
▪ 적용가능한 분야 : Market basket / Cross marketing / Catalog design / Biological Sequence
🧩 이렇게 Pattern Discovery의 개념에 대해서 간략하게 알아보았습니다. 이제 기본적인 용어들을 살펴봅시다.
🚩 2. Pattern Doscovery 기초
☑️ K - Itemsets and Support
▪ itemset : 하나 이상 itemset의 set
▪ K-itemset : K개로 구성된 itemset
📝 absolute-support
▪ sup{X}.
▪ itemset X의 출현빈도. 얼마나 많이 등장했는가.
▪ Frequency
📝 relative-support
▪ s{X}.
▪ itemset X를 포함한 transaction의 비율.
▪ $\frac{Sup}{total\;transaction}$
정리하면 absolute-support 는 itemset X의 빈도를 나타내고, relative-support 는 비율을 나타냅니다. 예제를 하나 가져와봤습니다.
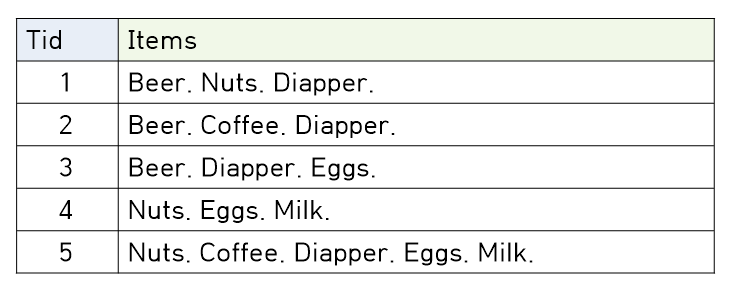
$sup\{Beer\}=3\;,\;\;\;s\{Beer\}=3/5=60\%$
$sup\{Diapper\}=4\;;,\;\;\;s\{Diapper\}=4/5=80\%$
$sup\{Beer,Diapper\}=3\;,\;\;\;s\{Beer,Diapper\}=3/5=60\%$
$sup\{Beer,Eggs\}=1\;,\;\;\;s\{Beer,Eggs\}=1/5=20%$
첨부한 표와 같은 데이터를 구매한 물품에 대한 정보를 담은 데이터라 해서 Transaction DB 라고 합니다.
☑️ Frequent Itemsets (Patterns)
▪ minsup : 임의로 설정한 relative-support의 임계값
▪ 만약 itemset X 의 relative-support s{X} 가 설정한 minsup 이상이면 X는 Frequent하다고 함.
▪ 즉, Transaction DB에서 함께, 자주 나타나는 K-itemset 을 어떻게 찾아낼 것인가에 대한 개념임.
이 개념 역시 예제를 한번 살펴봅시다!!

$Let\;\,minsup\;\;σ=50\%$
$s\{Beer\}=60\%\;,\;\;\;s\{Nuts\}=60\%$
$s\{Diapper\}=80\%\;,\;\;\;s\{Eggs\}=60\%$
$s\{Milk\}=40\%\;,\;\;\;s\{Beer,Diapper\}=60\%\;,\;\;\;s\{Nuts,Diapper\}=40\%$
위 예시에서 $minsup=50\%$ 이상의 frequent 한 itemset X는 {Beer} {Nuts} {Diapper} {Eggs} {Beer,Diapper}에 해당합니다. 반면 {Milk}는 40 으로 $minsup$ 보다 작기 때문에 frequent 하지 않습니다. 이때 2-itemset {Beer,Diapper} 가 frequent 하다는 것은 1-itemset {Beer}{Diapper} 각각 역시 frequent하다는 것을 의미합니다. 따라서 2-itemset의 frequent 를 판단함으로써 각 sub itemset의 frequent 역시 판단할 수 있습니다🙃🙃. 위의 예시에서 3개의 item 이 두 개 이상의 transaction에서 나오는 경우는 없기 때문에 2-itemset까지만 구해주었습니다.
☑️ Association Rule Mining
Association Rule Mining 에 대해서 알아보기 전에 알아야 할 개념이 하나 있습니다. 이 친구 먼저 슬쩍 살펴봅시다.
📝 Support
▪ transaction 이 $X\cup{Y}$를 contain 할 확률. 즉, $X,Y$ 두 itemset을 모두 포함할 확률.
▪ ex) $s{Beer,Diapper}=60%$
📝 Confidence
▪ conditional probability : $X\cup{Y}$에 대한 조건부확률
▪ $c=sup(X\cup{Y})/sup(X)$
▪ confidence 계산을 위해 사용하는 support는 absolute-support임에 유의.
▪ 표현은 $X\rightarrow{Y}(support,confidence)$로 한다.
- $X\rightarrow{Y}(s,c) : c=sup(X\cup{Y})/sup(X)$
- $Y\rightarrow{X}(s,c) : c=sup(X\cup{Y})/sup(Y)$
- $X\rightarrow{Y}(s,c)$에서 화살표의 시작 부분에 있는 itemset X가 confidence의 조건을 의미함.
support, confidence 라는 개념을 알아보았습니다. 이제는 Association Rule Mining을 알아보도록 합시다🙄.
Association Rule Mining 에서는 두 개의 임계치를 사용합니다. 아까 사용했던 minsup과 confidence에 대한 임계치인 minconf 입니다. 그 목적은 minsup과 minconf를 만족하는 연관성을 파악하는 것이며, 최종적으로 그 연관성을 나타내는 모든 rule을 찾는 것이 목적입니다.
📝 Association Rule Mining
▪ 두 개의 임계치 minsup, minconf 사용
▪ 함께 등장하는 itemset 간의 연관성을 파악해야 하므로 2-itemset이 존재해야 .
▪ Find all rules : $X\rightarrow{Y}(s,c)\;\;that\;\;s\geq{minsup}\;\;and\;\;c\geq{minconf}$
🧩 위에서 사용한 Transaction Data를 가지고 Association Rule을 찾아봅시다.
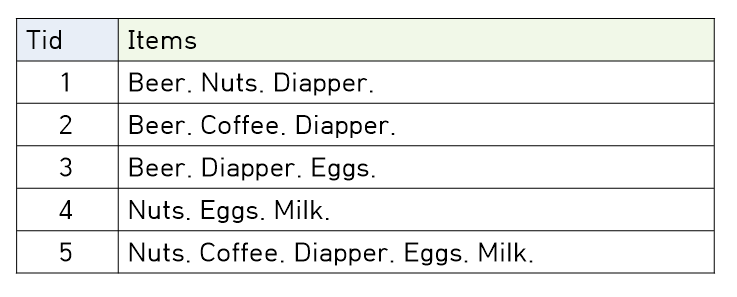
📌 우선 minsup을 만족하는 itemset을 먼저 찾아보도록 합시다.
$Let\;\,minsup\;\;σ=50\%$
$s\{Beer\}=60\%\;,\;\;\;s\{Nuts\}=60\%$
$s\{Diapper\}=80\%\;,\;\;\;s\{Eggs\}=60\%$
$s\{Milk\}=40\%\;,\;\;\;s\{Beer,Diapper\}=60\%\;,\;\;\;s\{Nuts,Diapper\}=40\%$
📌 이때 $minsup = 50\%$ 이상인 itemset은 {Beer} {Nuts} {Diapper} {Eggs} {Beer,Diapper} 입니다.
minsup을 만족하는 itemset을 찾았으니 이번에는 minconf를 만족하는 itemset을 찾아야 합니다.
두 임계치를 모두 만족하는 경우가 찾으려는 rule이기에, 위에서 찾은 itemset에서 confidence를 계산하면 됩니다.
$Let\;\,minconf\;\;σ=50\%$
$Beer\rightarrow{Diapper} : c=sup(Beer\cup{Diapper})/sup(Beer)=3/3=1$
$Diapper\rightarrow{Beer} : c=sup(Beer\cup{Diapper})/sup(Diapper)=3/4=0.75$
📌 이렇게 구한 support와 confidence로 Association Rule을 표현하면 아래와 같습니다.
$Beer\rightarrow{Diapper}(s,c)=(60\%,100\%)$
$Diapper\rightarrow{Beer}(s,c)=(60\%,75\%)$
📌 $Beer$와 $Diapper$ 각각이 선행조건인 경우 모두 minconf를 만족하기에, Association Rule은 다음과 같습니다.
$Beer\rightarrow{Diapper}\;\;\;and\;\;\;Diapper\rightarrow{Beer}$
🚩 3. 요약
🧩 이렇게 해서
▪ itemset
▪ absolute-support
▪ relative-support
▪ Frequent Itemsets
▪ Confidence
▪ Association Rule Mining
에 대해서 알아보았습니다.
🧩 결론적으로 Transaction Data 의 K-itemset 으로부터 support 와 confidence 를 구하고, 그 값들을 바탕으로 Association Rule Mining 을 만족하는 rule을 찾아보았습니다. 하지만 오늘 설명을 위해 사용한 예제는 2-itemset이 최대인 경우였기 때문에, 다음 포스팅에서는 frequent pattern이 너무 많은 경우에 대해 알아보도록 합시다🏃♂️🏃♂️.
🧩 전처리나 Classification, Clustering은 평소에 공부하면서 익숙한 느낌이 있었는데, 패턴분석은 처음 배운 내용이었고 오랜만에 공부하다 보니 많이 헷갈렸던 것 같습니다. 완전히 새로 배우는(...😨) 느낌이 나서 포스팅하는 데에 정말 많은 시간이 걸렸지만, 이렇게 정리하고 나니 그래도 어느 정도 정리되는 것 같아 좋았습니다. 앞으로의 패턴분석 내용이 이번 포스팅에서 다룬 개본적인 개념을 바탕으로 진행되기 때문에 나름 꼼꼼하게 정리했는데 어떨지 모르겠습니다. 아무쪼록 도움이 되면 좋겠네요ㅎㅎ🙂🙂.
💡위 포스팅은 한국외국어대학교 바이오메디컬공학부 고윤희 교수님의 [생명정보학을 위한 데이터마이닝] 강의를 바탕으로 합니다.