모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

🩸 저번 글에 이어 이번 글에서는 Decisioin Tree를 통해 각 데이터프레임의 accuracy를 비교해봅시다.
🩸 먼저 사용할 데이터를 확인하겠습니다.
📌 전처리한 데이터

📌 PCA 데이터프레임

🫀 1. Original Data
🩸 먼저 가져온 데이터의 target을 범주형으로 변경해봅시다.
cardio.target_rand = cardio['cardio'].copy()
cardio.target_rand[cardio.target_rand==0] = 'N'
cardio.target_rand[cardio.target_rand==1] = 'Y'
🩸 이제 앞선 연관관계 분석에서 추출한 attribute들을 가지고 각각의 경우에 해당하는 데이터프레임을 만들겠습니다.
# 1. 전체 feature 사용
cardio_1_feat = cardio.drop(['cardio'], axis = 1).copy()
# 2. [aphi, aplo, cholesterol, BMI]
cardio_2_feat = cardio.drop(['cardio','age','gender','gluc','smoke','alco','active'], axis = 1).copy()
#3. [age, aphi, aplo, cholesterol, BMI]
cardio_3_feat = cardio.drop(['cardio','gender','gluc','smoke','alco','active'], axis = 1).copy()
#4. [age, aphi, aplo, cholesterol, gluc, BMI]
cardio_4_feat = cardio.drop(['cardio','gender','smoke','alco','active'], axis = 1).copy()
#5. [age, aphi, aplo, cholesterol, gluc, BMI, active]
cardio_5_feat = cardio.drop(['cardio','gender','alco','smoke'], axis = 1).copy()
#6. [aphi, aplo, cholesterol, gluc, BMI]
cardio_6_feat = cardio.drop(['cardio','gender','alco','smoke','age','active'], axis = 1).copy()
각 데이터가 가지고 있는 attribute들이 다르기 때문에 일일이 모델을 만드는 게 상단히 번거로운 일이라고 생각했습니다. 따라서 이를 간단하게 만들어주는 함수를 정의하였습니다.
추출한 attribute 만으로 구성된 데이터프레임과 결정트리의 깊이를 인수로 받아 train set과 test set의 accuracy를 반환하는 함수를 만들어 주었습니다.
def predict_accuracy(features, depth):
x_train, x_test, y_train, y_test =
train_test_split(features, cardio.target_rand, test_size=0.3, random_state=1)
# 데이터 표준화 작업
sc = StandardScaler()
sc.fit(x_train)
# 표준화된 데이터셋
x_train_std = sc.transform(x_train)
x_test_std = sc.transform(x_test)
# 종속변수가 현재 범주형
clf_train = tree.DecisionTreeClassifier(criterion="entropy",max_depth=depth)
clf_train = clf_train.fit(x_train,y_train)
# 종속변수가 현재 범주형
clf_test = tree.DecisionTreeClassifier(criterion="entropy",max_depth=depth)
clf_test = clf_test.fit(x_train,y_train)
y_pred_tr_train = clf_train.predict(x_train)
y_pred_tr_test = clf_test.predict(x_test)
return clf_train,
accuracy_score(y_train, y_pred_tr_train),
clf_test,
accuracy_score(y_test, y_pred_tr_test)
🩸 이 함수를 가지고 accracy를 계산해봅시다.
🚩 1.1. max_depth = None 결과 해석
# max_depth = None 인 경우의 train set accuracy와 test set accuracy
print('Case 1 train Accuracy: %.5f' % predict_accuracy(cardio_1_feat, None)[1])
print('Case 1 test Accuracy: %.5f' % predict_accuracy(cardio_1_feat, None)[3], '\n')
print('Case 2 train Accuracy: %.5f' % predict_accuracy(cardio_2_feat, None)[1])
print('Case 2 test Accuracy: %.5f' % predict_accuracy(cardio_2_feat, None)[3], '\n')
print('Case 3 train Accuracy: %.5f' % predict_accuracy(cardio_3_feat, None)[1])
print('Case 3 test Accuracy: %.5f' % predict_accuracy(cardio_3_feat, None)[3], '\n')
print('Case 4 train Accuracy: %.5f' % predict_accuracy(cardio_4_feat, None)[1])
print('Case 4 test Accuracy: %.5f' % predict_accuracy(cardio_4_feat, None)[3], '\n')
print('Case 5 train Accuracy: %.5f' % predict_accuracy(cardio_5_feat, None)[1])
print('Case 5 test Accuracy: %.5f' % predict_accuracy(cardio_5_feat, None)[3], '\n')
print('Case 6 train Accuracy: %.5f' % predict_accuracy(cardio_6_feat, None)[1])
print('Case 6 test Accuracy: %.5f' % predict_accuracy(cardio_6_feat, None)[3], '\n')>>
Case 1 train Accuracy: 0.97181
Case 1 test Accuracy: 0.64212
Case 2 train Accuracy: 0.82638
Case 2 test Accuracy: 0.65860
Case 3 train Accuracy: 0.94109
Case 3 test Accuracy: 0.64300
Case 4 train Accuracy: 0.94673
Case 4 test Accuracy: 0.64134
Case 5 train Accuracy: 0.95736
Case 5 test Accuracy: 0.64382
Case 6 train Accuracy: 0.84334
Case 6 test Accuracy: 0.65659
max_depth = None 의 결과 train set의 accuracy와 test set의 accuracy의 차이가 크기 때문에 오버피팅이 일어났다고 예측할 수 있습니다. 따라서 Pruning을 통한 오버피팅 조정의 필요성을 느꼈습니다.
🚩 1.2. max_depth = 5 결과 해석
# max_depth = 5 인 경우의 train set accuracy와 test set accuracy
print('Case 1 train Accuracy: %.5f' % predict_accuracy(cardio_1_feat, 5)[1])
print('Case 1 test Accuracy: %.5f' % predict_accuracy(cardio_1_feat, 5)[3], '\n')
print('Case 2 train Accuracy: %.5f' % predict_accuracy(cardio_2_feat, 5)[1])
print('Case 2 test Accuracy: %.5f' % predict_accuracy(cardio_2_feat, 5)[3], '\n')
print('Case 3 train Accuracy: %.5f' % predict_accuracy(cardio_3_feat, 5)[1])
print('Case 3 test Accuracy: %.5f' % predict_accuracy(cardio_3_feat, 5)[3], '\n')
print('Case 4 train Accuracy: %.5f' % predict_accuracy(cardio_4_feat, 5)[1])
print('Case 4 test Accuracy: %.5f' % predict_accuracy(cardio_4_feat, 5)[3], '\n')
print('Case 5 train Accuracy: %.5f' % predict_accuracy(cardio_5_feat, 5)[1])
print('Case 5 test Accuracy: %.5f' % predict_accuracy(cardio_5_feat, 5)[3], '\n')
print('Case 6 train Accuracy: %.5f' % predict_accuracy(cardio_6_feat, 5)[1])
print('Case 6 test Accuracy: %.5f' % predict_accuracy(cardio_6_feat, 5)[3], '\n')>>
Case 1 train Accuracy: 0.72678
Case 1 test Accuracy: 0.72439
Case 2 train Accuracy: 0.72246
Case 2 test Accuracy: 0.71824
Case 3 train Accuracy: 0.72698
Case 3 test Accuracy: 0.72398
Case 4 train Accuracy: 0.72795
Case 4 test Accuracy: 0.72439
Case 5 train Accuracy: 0.72678
Case 5 test Accuracy: 0.72439
Case 6 train Accuracy: 0.72277
Case 6 test Accuracy: 0.71866
max_depth = None 인 경우에 비해 train set과 test set 사이의 accuracy 차이가 확연히 줄어들었습니다. Pruning에 의해 오버피팅은 해결된 것으로 보이지만, 전체적으로 accuracy가 높은 값은 아니기 때문에 다른 calssification algorithm이 필요할 것이라 생각했습니다.
🫀 2. PCA Data
PCA Data 의 경우에는 우선 동일하게 target을 범주형으로 바꿔준 후, 어느 깊이에서 결정 트리가 가장 좋은 값을 보여주는지 시각화를 해보겠습니다. 이렇게 얻어낸 값으로 accuracy를 계산해봅시다.
PCA_df.target = PCA_df['cardio'].copy()
PCA_df.target[PCA_df.target==0] = 'N'
PCA_df.target[PCA_df.target==1] = 'Y'
PCA_df.feat = PCA_df.drop(['cardio'], axis = 1).copy()
x_train_PCA, x_test_PCA, y_train_PCA, y_test_PCA =
train_test_split(PCA_df.feat, PCA_df.target, test_size=0.2, random_state=1)
# Information Gain - entropy
clf_PCA = tree.DecisionTreeClassifier(criterion = "entropy", max_depth=6)
clf_PCA = clf_PCA.fit(x_train_PCA, y_train_PCA)
# 깊이에 따른 시각화
accuracy_df = pd.DataFrame()
for i in range(1,20):
a = tree.DecisionTreeClassifier(criterion = "entropy", max_depth=i)
a = a.fit(x_train_PCA, y_train_PCA)
b = a.predict(x_test_PCA)
accuracy_df = accuracy_df.append(pd.DataFrame
({'accuracy' : (accuracy_score(y_test_PCA, b)).round(5)}, index = [i]))
px.line(
x=range(1,20),
y=accuracy_df['accuracy'],
labels={"x": "max_depth", "y": "Accuracy"}
)
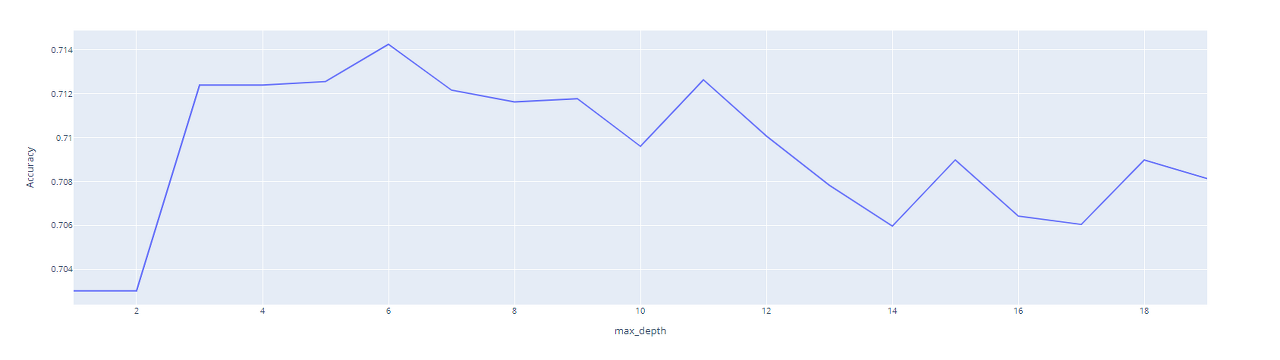
🚩 2.1. PCA 결과해석
🩸 앞선 시각화 결과 깊이가 6 일때 가장 좋은 accuracy를 가졌기 때문에 max_depth = 6 인 경우의 결과를 해석합니다.
x_train_PCA, x_test_PCA, y_train_PCA, y_test_PCA =
train_test_split(PCA_df.feat, PCA_df.target, test_size=0.2, random_state=1)
# Information Gain - entropy
clf_PCA = tree.DecisionTreeClassifier(criterion = "entropy", max_depth=6)
clf_PCA = clf_PCA.fit(x_train_PCA, y_train_PCA)
# max_depth = 6 인 경우의 train set / test set accuracy
y_pred_tr_PCA_test = clf_PCA.predict(x_test_PCA)
y_pred_tr_PCA_train = clf_PCA.predict(x_train_PCA)
print('PCA train Accuracy: %.5f' % accuracy_score(y_train_PCA, y_pred_tr_PCA_train))
print('PCA test Accuracy: %.5f' % accuracy_score(y_test_PCA, y_pred_tr_PCA_test))>>
PCA train Accuracy: 0.72171
PCA test Accuracy: 0.71419
PCA를 진행했음에도 앞서 추출한 attribute를 가지고 max_depth를 5로 설정하였을 때의 original data 결과와 큰 차이가 없습니다. 따라서 다른 classification algorithm이 필요할 것이라고 생각했습니다.
🩸 이렇게 결정 트리를 통한 각 데이터들의 accuracy를 구해보았습니다.
🩸 하지만 결정트리만 가지고 데이터의 target을 예측하기는 어려웠습니다. 따라서 다른 calssification 방법을 사용하기로 했습니다.
🩸 다음 글에서는 이렇게 만든 결정 트리를 시각화해보겠습니다.
'🐍 파이썬 데이터 분석 프로젝트 > 🫀 심혈관질환 데이터 분석' 카테고리의 다른 글
| 🫀 심혈관질환 데이터 분석 15. 랜덤포레스트 (4) | 2023.02.04 |
|---|---|
| 🫀 심혈관질환 데이터 분석 14. 결정트리 시각화 (0) | 2023.02.03 |
| 🫀 심혈관질환 데이터 분석 12. 라이브러리 임포트 (0) | 2023.02.03 |
| 🫀 심혈관질환 데이터 분석 11. plotly 차트보드 (0) | 2023.02.02 |
| 🫀 심혈관질환 데이터 분석 10. 주성분분석 (0) | 2023.02.02 |