모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

이번 포스팅에서는 Dimensionality Reduction 중의 Principal Component Analysis, 주성분분석에 대해서 알아보도록 합시다🙃.
🚩1. PCA - Dimensionality Reduction
데이터마이닝 분야에 조금이라도 관심이 있거나, 관련된 서적을 읽어보신 분들은 PCA 라는 말을 이래저래 많이 접해보셨을 것입니다. 오늘 알아볼 Principal Component Analysis를 줄여서 부른 게 바로 PCA 분석입니다. 그만큼 유명하고, 데이터 분야에서는 떼어놓을 수 없을 만큼 중요하지만 여러 데이터마이닝 프레젠테이션을 봤을 때 PCA가 무엇인지, 왜 하는지에 대해 정확히 알고 대답하는 것을 들은 적은 잘 없습니다. 또한 인터넷을 찾아보아도 대부분 수식이나 머신러닝에 사용되는 PCA를 다루고 있습니다. 데이터마이닝 공부를 할 때 필요한 정확한 개념에 대해 다루는 내용은 거의 본 적이 없기에, 이번 포스팅에서는 PCA의 가장 기본적인 개념에 대해 다루도록 하겠습니다.
데이터마이닝 과목을 수강할 때 사용한 교재에서는 PCA를 아래와 같이 정의합니다.
Transfer a set of correlated variables into a new set of uncorrelated variables.
이를 단순히 번역해보면 관련된 변수들을 서로 관련이 없는 변수들의 set으로 변환한다는 내용인데, 사실 위의 정의만 보고 정확한 개념을 이해하기는 어렵습니다. 그래서 교수님께도 질문드려보고, 관련된 글들을 찾아 읽은 결과 제 나름대로 PCA의 정의를 아래와 같이 정리해보았습니다.
기존의 attributes를 linear combination해서 새로운 attributes를 만드는 것.
그리고 그 새로운 attributes가 새로운 축인 principal component (PC)로 정의됨.
기존의 데이터들은 새로운 축 PC1, PC2...에서 새로운 좌표를 가지게 됨.
이렇게 원래 attribute들을 linear combination등의 연산을 통해 combine하는 과정에서 자연스럽게 데이터가 간략해지고, 그 dimension 역시 줄어든다는 의미입니다. 이를 그림으로 나타내면 아래와 같습니다.
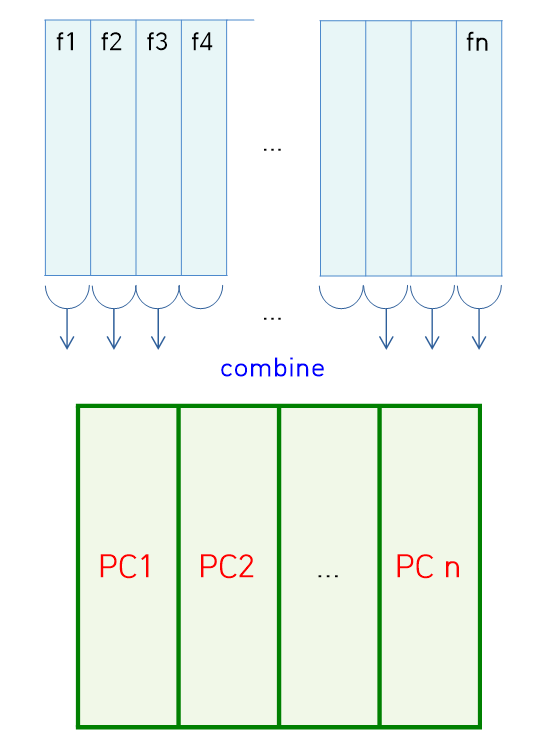
위의 그림에서 새롭게 만들어진 데이터의 각각의 attribute인 PC1, PC2,...가 새롭게 좌표를 만들기 위한 축을 형성하게 되고, 원래 가지고 있던 데이터는 새로운 좌표평면에서 표현됩니다. 그렇다면 이제 하나의 질문이 생깁니다. 새로운 attribute를 만드는 것은 이해가 가는데, 그러면 그 순서는 어떻게 정해지는 것일까요🙄??
🚩 2. PCA - New Axis
그렇다면, 이제 위의 질문에 대한 대답과 전반적인 PCA분석의 결과를 알아봐야겠습니다.
가장 먼저 위의 질문에 대한 답을 하자면, 새로운 attribute는 기존 데이터의 variance를 가장 잘 설명할 수 있는 축의 순서대로 숫자를 붙여 나갑니다. 이 전후관계를 혼동하지 않으시면 좋겠는데, 만들 때 마다 순서를 매기는 것이 아니라 새로운 축들을 만든 뒤에 그 축들을 기준으로 원래 데이터의 variance를 잘 설명하는 순서대로 번호를 매기는 것입니다. 즉 PC1 이 원본 데이터의 variance를 가장 잘 나타낼 수 있고, 그 다음은 PC2가, 그 뒤는 PC3가... 이런 순서대로 이름을 붙여나가는 것입니다.
attribute를 combine해서 새로운 축을 만들 때 중요한 점이 있습니다. 앞서 언급했듯 저희는 새로운 축을 바탕으로 원래 데이터에 새로운 좌표를 부여합니다. 이때 저희가 흔히 알고 있는 xy평면을 예로 들어보면, 두 축은 서로 직교합니다. 즉, 서로 orthogonal 합니다. 따라서 데이터를 새로운 평면에서 표현하기 위해, 새로운 축들인 Principal Component들 또한 서로 orthogonal 해야합니다.
선형대수학을 알고 계신다면 eigen vector와 eigen value에 대해서 알고 있으실 것입니다. 간략히 설명드리자면 정사각 행렬 A가 주어졌을 경우에 적당한 수 λ에 대하여 Ax=λx를 만족하는 zero vector 이외의 벡터 x를 eigen vector라 하고, 이때 곱해지는 적당한 수 λ를 eigen value라고 합니다. 그리고 PCA 에서는 데이터의 variance를 설명하기 위해서 각각의 Principal Component (eigen vector)에 서로 다른 수(eigen value)가 곱해지는데, 이 eigen value가 가장 큰 Principal Component부터 PC1, PC2,... 이렇게 이름을 붙이게 됩니다.
보다 쉬운 이해를 위해서 아래 그림을 참고하시면 좋을 것 같습니다🙂🙂.
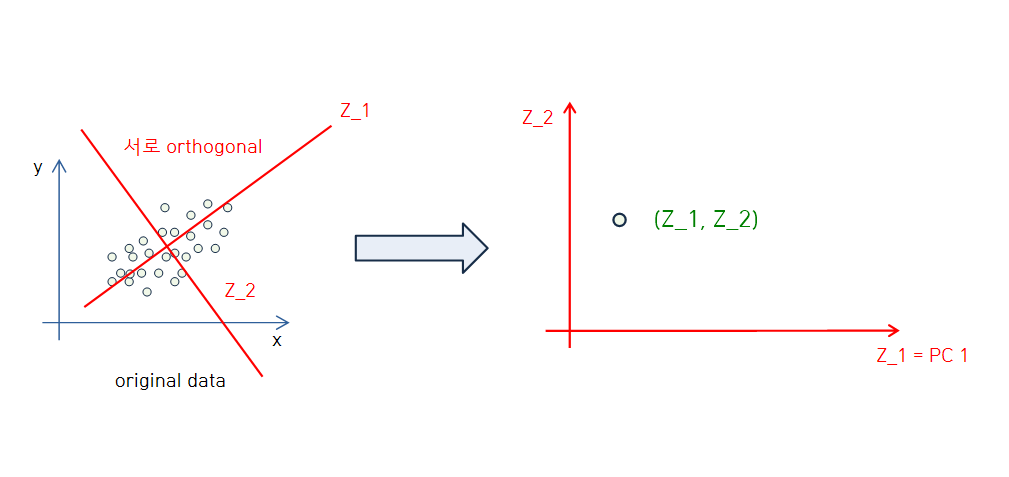
위의 그림에서 확인 할 수 있듯이
- PC1과 PC2... 는 서로 orthogonal 합니다.
- 원래 데이터가 Principal Component로 만들어진 좌표평면에서 새롭게 표현됩니다.
위의 그림에서 원본 데이터에서는 point가 여러개인데 새로운 평면으로 옮겼을때 점을 하나만 그려두었다고 해서 원본 데이터가 단 하나의 점으로 표현되는 것이 아닙니다!! 저와 이 글을 읽으시는 분들이 보다 잘 보실 수 있도록 저렇게 표현한 것입니다🙃🙃.
앞서 설명했듯 원래 데이터의 variance 설명 정도를 기준으로 Principal Component의 넘버링을 정의하는데, 이에 따라 대부분의 variance가 PC1과 PC2만 가지고서 설명이 가능합니다. 이때 PC1과 PC2만을 가지고 설명이 되지 않은 경우에는 PC3,PC4... 까지 사용하면 표현이 가능합니다. 또한, 원하는 설명 정도가 나올때까지 Principal Component를 선택하고 합치는 것도 가능합니다. 이와 관련된 내용은 2022년도 1학기에 진행한 (영혼을 갈아 넣은) 데이터마이닝 프로젝트를 통해 다음 포스팅에서 설명할 생각입니다🙄.
앞서 PCA를 통해 원래 attribute를 combine하는 과정에서 데이터의 dimension이 줄어든다고 설명했습니다. 하지만 이에 더해서 PCA는 dimension을 줄일 수 있다는 큰 장점이 있습니다. 이는 Principal Component를 선택하는 과정을 통해서 이루어집니다. 원하는 정도까지만 variance를 설명하면 되고, 이를 만족하는 Principal Component까지만 선택할 것이기 때문에, 이를 선택하는 과정에서 자연스럽게 Dimensionality Reduction을 하게 되는 것입니다.
🧩 이렇게 PCA에 대해 중요한 개념을 나름 자세히 짚어보았습니다. 이번 포스팅의 내용을 요약하면 아래와 같습니다.
▪ 기존의 attributes를 linear combination해서 새로운 attributes를 만드는 것.
▪ 만든 새로운 attributes가 새로운 축인 principal component로 정의됨.
▪ 기존의 데이터들은 새로운 축 PC1, PC2...에서 새로운 좌표를 가지게 됨.
▪ 새로운 축들을 기준으로 만든 좌표평면에서 원래 데이터의 variance를 잘 설명하는 순서대로 번호를 매김.
▪ 각각의 만들어지는 새로운 축들인 Principal Component들 또한 서로 orthogonal 해야함.
▪ 대부분의 variance가 PC1과 PC2만 가지고서 설명이 가능함.
▪ 원하는 설명 정도가 나올때까지 Principal Component를 선택하고 합치는 것도 가능함.
▪ 원하는 정도의 variance를 설명하는 Principal Component 까지만 선택하는 과정에서 Dimensionality Reduction이 가능함.
🧩 실제로 PCA에 관련된 연산은 우리의 소중한 컴퓨터가 해줄 것이기 때문에, 이번에 배운 개념들만 아주 소중히 머리에 간직해도 PCA가 무엇이냐는 질문에 당황하지 않고 대답할 수 있을 거라고 생각합니다🙂!! 다음 포스팅에서는 실제로 PCA를 하는 과정과 결과에 대해서 알아보도록 합시다🏃♂️🏃♂️🏃♂️.
💡위 포스팅은 한국외국어대학교 바이오메디컬공학부 고윤희 교수님의 [생명정보학을 위한 데이터마이닝] 강의를 바탕으로 합니다.
'📌 데이터마이닝 > 데이터 전처리' 카테고리의 다른 글
| 🚩 데이터마이닝 18. Data Transformation (0) | 2023.02.21 |
|---|---|
| 🚩 데이터마이닝 17. Reduction - 주성분분석 구현 (0) | 2023.02.20 |
| 🚩 데이터마이닝 15. Reduction - Subset Selection (0) | 2023.02.19 |
| 🚩 데이터마이닝 14. Dimensionality Reduction (0) | 2023.02.19 |
| 🚩 데이터마이닝 13. Reduction - Nonparametric (0) | 2023.02.17 |