모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

이번 글에서는 프로젝트 내용을 통해 PCA, 즉 주성분 분석을 통한 attribute 간의 연관관계를 살펴보겠습니다.
🚩 1. PCA 코드 구현
sklearn.decomposition 모듈의 PCA 라이브러리 를 사용했고, 시각화를 위해 plotly 공식 홈페이지를 참고했습니다.
🚩 1.1. 데이터 확인

위 데이터를 가지고 PCA를 진행하겠습니다.
🚩 1.2. PCA 구현 및 시각화_Princiapl Component 1~3
📌 먼저 코드부터 확인해보겠습니다🙄.
# target과 feature data 설정
# cardio가 0인 object는 'N' 으로 변환
# cardio가 1인 object는 'Y' 로 변환
cardio_target = cardio['cardio'].copy()
cardio_target[cardio_target==0] = 'N'
cardio_target[cardio_target==1] = 'Y'
cardio_feat = cardio.drop('cardio',axis = 1)# sklearn.decomposition 모듈의 PCA library 임포트
# pca.fit_transform() : cardio[features]를 scaling 한 뒤에 principal component로 변환
# pca.explained_variance_ratio_ : dimension에 따른 variance 설명 정도
pca = PCA()
components = pca.fit_transform(cardio_feat)
# PCA 결과 시각화
labels = {
str(i): f"PC {i+1} ({var:.1f}%)"
for i, var in enumerate(pca.explained_variance_ratio_ * 100)
}
fig = px.scatter_matrix(
components,
labels=labels,
dimensions=range(3),
color=cardio_target, opacity = 0.5
)
fig.update_traces(diagonal_visible=False)
fig.show()
PCA 과정에서 만들어지는 Principal Component의 수에 따라 원본 데이터의 variance 설명 정도가 결정되기에 dimension을 결정하는 변수가 존재합니다. 위 코드에서 dimensions = range(3) 가 그 변수이며, 이를 통해 PCA 결과를 시각화하면 아래와 같습니다.

그 결과 target으로 설정한 cardio attribute가 각각 3개의 차원에서 설명되는 것을 확인할 수 있으며, PC1과 PC2에서 대부분의 variance가 설명되는 것을 확인할 수 있습니다🙃. PCA를 공부한 분이라면 아시겠지만 위의 결과는 target label에 따라 선명하게 분류된 경우는 아닙니다. 각 attribute에 따라 target label이 명확하게 결정된다면, 위의 경우처럼 점들이 겹치기보다는 명확히 구분되는 결과가 나오게 되며, PC1에서 90%가 넘는 설명정도를 가집니다. 하지만 이는 데이터의 차이라고 볼수 있기 때문에, 아쉽긴 하지만 그렇게 신경쓸 부분은 아닐 것이라 생각하고 프로젝트를 진행했습니다.
이번에는 dimension이 4인 경우를 살펴보도록 하겠습니다.
🚩 1.3. PCA 구현 및 시각화_Princiapl Component 1~4
# 사용하려는 principal componenet 개수 정의
n_components = 4
# sklearn.decomposition 모듈의 PCA library 임포트. principal componenet 개수 정의.
# pca.fit_transform() : cardio[features]를 scaling 한 뒤에 principal component로 변환
# pca.explained_variance_ratio_ : dimension에 따른 variance 설명 정도
pca = PCA(n_components=n_components)
components = pca.fit_transform(cardio)
# PCA 결과 시각화
total_var = pca.explained_variance_ratio_.sum() * 100
labels = {str(i): f"PC {i+1}" for i in range(n_components)}
fig = px.scatter_matrix(
components,
color=cardio_target,
opacity = 0.5,
dimensions=range(n_components),
labels=labels,
title=f'Total Explained Variance: {total_var:.2f}%',
)
fig.update_traces(diagonal_visible=False)
fig.show()
위의 코드는 앞선 코드와 달리 n_components 변수를 통해 princiapl component의 개수를 미리 설정해두고 PCA를 진행합니다. 그 결과는 아래 그림과 같습니다.
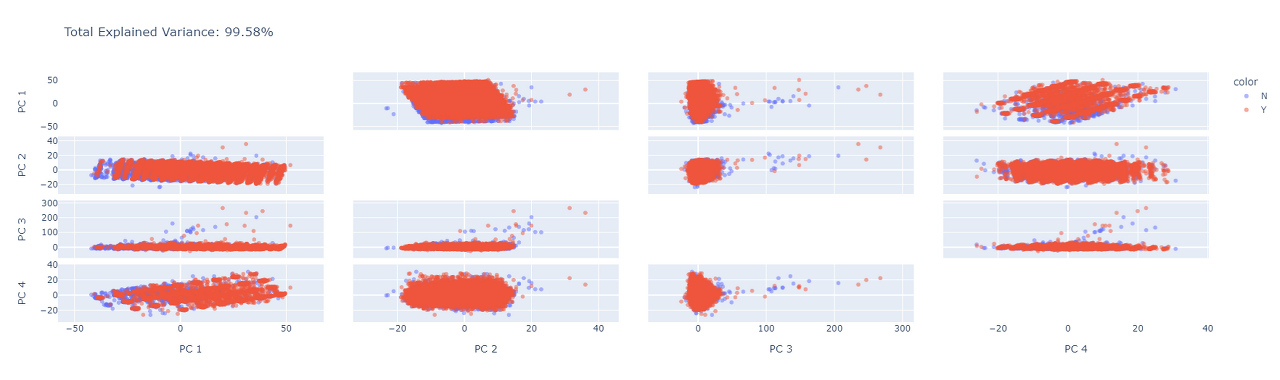
PC4 까지 사용한 경우에 원본 데이터의 variance를 99.58% 까지 설명하는 것을 확인했고, 이에 PCA 분석을 위해 dimension을 4로 설정하기로 했습니다. 당연히 PC의 수가 늘어날수록 설명 정도는 증가할 것이기에, 이를 확인해보기 위해서 시각화를 진행하였습니다.
# dimension에 따른 variance 설명 정도의 누적합 시각화
pca = PCA()
pca.fit(cardio)
exp_var_cumul = np.cumsum(pca.explained_variance_ratio_)
px.area(
x=range(1, exp_var_cumul.shape[0] + 1),
y=exp_var_cumul,
labels={"x": "# Components", "y": "Explained Variance"}
)

이 결과를 토대로 dimension을 4로 설정해서 각 attribute 간의 연관관계를 알아보겠습니다.
🚩 1.4. attribute 연관관계 파악
PCA에 대한 개념만 가지고 실제로 연관관계를 어떻게 분석하는지 알기는 어렵습니다.
이를 위해 사이킷런과 plotly 에서는 각 attribute의 방향성을 파악하기 위한 여러 기능을 제공합니다.
# vardiance를 설명하는 데 사용된 original attribute vector의 방향성 파악
X = cardio[cardio_feat.columns]
pca = PCA(n_components=4)
components = pca.fit_transform(X)
loadings = pca.components_.T * np.sqrt(pca.explained_variance_)
fig = px.scatter(components, x=0, y=1, color=cardio_target, opacity = 0.5)
for i, feature in enumerate(X):
fig.add_shape(
type='line',
x0=0, y0=0,
x1=loadings[i, 0],
y1=loadings[i, 1],
line=dict(color="springgreen",width=3.5)
)
fig.add_annotation(
x=loadings[i, 0],
y=loadings[i, 1],
ax=0, ay=0,
xanchor="center",
yanchor="bottom",
text=feature,
font = {'color':'white'},
bgcolor = 'grey'
)
fig.show()
loadings 변수 를 통해 각 attribute vector의 방향을 나타낼수 있도록 했고, for 문을 사용해서 모든 point와 vector를 시각화했습니다. 그 결과는 아래와 같습니다.

이 결과만 가지고 정확한 attribute의 방향성을 파악하기에는 각 vector가 너무 겹쳐있기 때문에, plotly에서는 이를 확대해서 볼 수 있는 기능을 제공합니다. 확대해보면 다음과 같습니다.

📌 PCA 분석의 결과 서로 가장 연관관계가 가장 높은 attribute는 다음과 같이 결정됐습니다.
ap_hi, ap_lo, BMI, gluc, cholestero
🚩 1.5. PCA DataFrame
마지막으로 위에서 선택된 attribute를 가지고 PCA DataFrame을 만들겠습니다🙂.
# PCA Dataframe 출력
pca = PCA(n_components=n_components)
components = pca.fit_transform(cardio)
PCA_df = pd.DataFrame({'PC1' : components[:,0],
'PC2' : components[:,1],
'PC3' : components[:,2],
'PC4' : components[:,3],
'cardio' : cardio['cardio']})
PCA_df
🚩 2. PCA 정리
PCA를 통한 상관관계 분석의 결과는 아래와 같이 정리할 수 있습니다.
▪ PCA 결과 총 4개의 pricipal component로 99.58%의 variance를 설명할 수 있습니다.
▪ original attribute의 방향성을 살펴보면 선택된 attribute가 유사한 방향으로 나아가고 있는 것을 확인할 수 있습니다.
프로젝트 진행 과정에서 도움을 받은 사이트와 제가 운영한 블로그의 plotly 라이브러리 포스팅을 공유할테니 궁금하신 분들은 참고하시면 좋을 것 같습니다🙃🙂.
Pca
Detailed examples of PCA Visualization including changing color, size, log axes, and more in Python.
plotly.com
📊 시각화 02. plotly
📝 목차 1. plotly 1.1. plotly 사용하기 1.2. 기본형태 1.2.1. fig.add_trace( ) 1.2.2. fig.update_layout( ) 1.2.3. fig.add_annotation( ) 1.2.4. fig.show( ) 1.3. 코드 예시 1. plotly 📊 이번 포스팅에서는 iplot보다 세심하게 시각
nyamin9-data.tistory.com
📊 시각화 03. plotly에서 for문 사용하기
📝 목차 1. for 문을 사용하지 않은 plotly 2. for 문으로 plotly 그려보기 📊 오늘은 plotly에서 for loop를 사용하는 법을 알아봅시다. 📊 단순히 여러개의 그래프를 그리는 것이 아닌 각각의 데이터 요
nyamin9-data.tistory.com
🚩 데이터마이닝 16. Reduction - 주성분분석(PCA)
🆘 모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!! 이번 포스팅에서는 Dimensionality Reduction 중의 Principal Component Analysis, 주성분분석
nyamin9-data.tistory.com
'📌 데이터마이닝 > 데이터 전처리' 카테고리의 다른 글
| 🚩 데이터마이닝 19. 데이터 전처리 리뷰 (0) | 2023.02.24 |
|---|---|
| 🚩 데이터마이닝 18. Data Transformation (0) | 2023.02.21 |
| 🚩 데이터마이닝 16. Reduction - 주성분분석(PCA) (0) | 2023.02.20 |
| 🚩 데이터마이닝 15. Reduction - Subset Selection (0) | 2023.02.19 |
| 🚩 데이터마이닝 14. Dimensionality Reduction (0) | 2023.02.19 |