모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

🧩 저번 포스팅에서 Data Cleaning에 대해서 간단하게 알아보았습니다. 이제는 본격적인 전처리를 위한 방법들을 배워나갈 것인데, 먼저 categorical data 의 integration을 위한 chi-square test를 알아보도록 합시다. 들어보신 분들은 아마 카이제곱검정 이 더 익숙하실 것 같습니다.
🚩 1. Data Integration
기업이나 큰 데이터베이스에서 Data Integration은 여러 출처의 데이터를 일관된 저장소로 통합하거나 데이터베이스를 통합하여 각각의 데이터를 워래의 범위보다 축소된 범위에서 한번에 다루기 위한 방법으로 정의됩니다.
일반적으로는 데이터의 attribute를 통합하여 복잡한 연산을 줄이거나 데이터의 dimension을 줄여 분석한다는 의미입니다.
앞으로 알아볼 다양한 measure들은 attribute의 Integration을 위한 기준을 정하는 것이라 이해하시면 될 듯 합니다.
🚩 2. Categorical Data : chi-square test (카이제곱검정)
이제 첫번째 measure를 알아보겠습니다.
첫번째 방법은 범주형 데이터의 통합을 위한 chi-square test (카이제곱검정) 입니다.
카이제곱검정을 통해 $attirubute_i$와 $attribute_j$ 간에 연관성이 있는지 알아보기 위해서는 한 가지 가설이 필요합니다.
이를 Null 가설이라고 부를 것입니다.
Null 가설 : 두 attribute i, j가 서로 독립이다. 즉, 서로 아무런 연관성이 없다.
📝 $χ^{2}-test$

각 attribute A와 B가 i, j의 case를 가질때 통계값은 다음과 같이 구해집니다.
$$e_{ij} = \frac{count(A=a_i)\times{count(B=b_j)}}{n},\;\;\;\;\, χ^{2} = \sum_{i=1}^c\sum_{j=1}^r\frac{(o_{ij}-e_{ij})^2}{e_{ij}}$$
$e_{ij}$를 구할 때 Null 가설이 적용됩니다.
즉, $e_{ij}$는 두 attribute가 서로 독립이라는 가정 하에 구해지는 통계값이고,
$o_{ij}$는 어떠한 가정 없이 표본의 조사 결과 구해지는 실제 값입니다.
즉, $o_{ij}$ (실제 관측값)와 $e_{ij}$ (독립 가정에 의한 값)의 차이가 크면 attribute i와 j는 서로 독립이 아니라는 것을 의미합니다.
따라서 $χ^{2}$ 가 클수록 두 attribute간의 correlation이 큽니다.
$χ^{2}$ 의 연산식을 보면 아시겠지만, 두 시그마의 위끝이 다릅니다. 즉, 각각의 attribute가 가지는 case의 수에 상관없이 chi-square 값을 계산할 수 있다는 의미입니다. 따라서 attribute간 상관관계 파악에 있어 상당히 효율적인 방법이라 말할 수 있을 것입니다.
👉 가볍게 에시를 한번 살펴보고 마무리하도록 합시다.
🚩 3. chi-square test 예제
성별 attribute A와 어떤 정책에 대한 찬성 / 반대 case를 가지는 attribute B 간의 correlation을 구해봅시다.

각 attribute를 정리한 값은 위의 표와 같습니다. 이를 바탕으로 각각의 $e_{ij}$를 구해봅시다.
$e_{11} = \frac{M\times{Y}}{n} = \frac{450\times{300}}{1500}=90$
$e_{21} = \frac{F\times{Y}}{n} = \frac{1050\times{300}}{1500}=210$
$e_{12} = \frac{M\times{N}}{n} = \frac{450\times{1200}}{1500}=360$
$e_{22} = \frac{F\times{N}}{n} = \frac{1200\times{1050}}{1500}=840$
이제 이 값들로 chi-square 값을 구해주면 됩니다. 각 $e_{ij}$를 표에 넣어 정리해보았습니다.
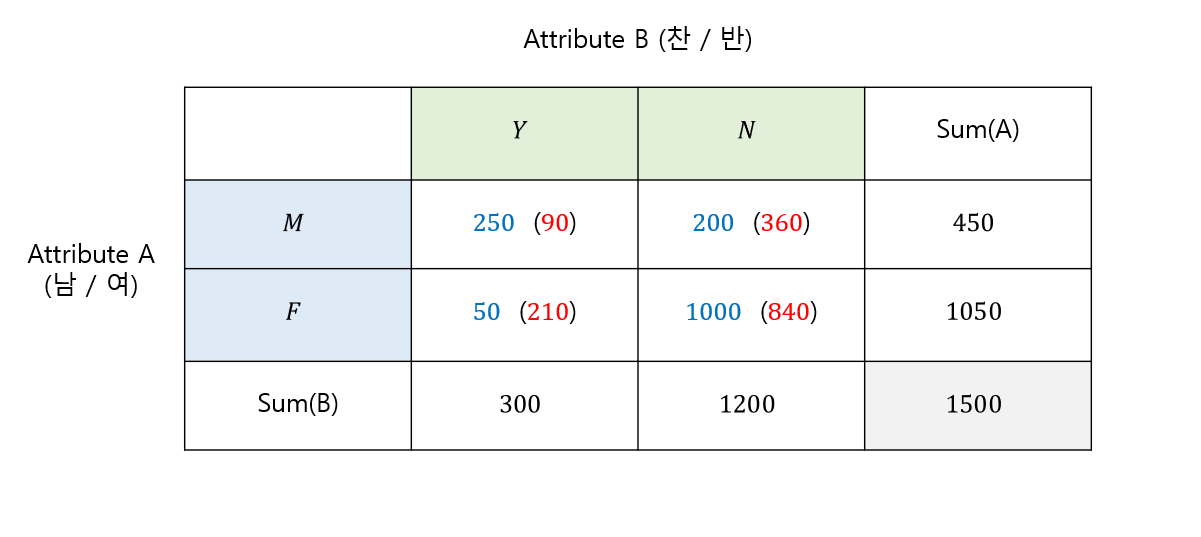
마지막으로 chi-square값을 구해줍시다.
$χ^{2} = \frac{(250-90)^2}{90}+\frac{(200-360)^2}{360}+\frac{(50-210)^2}{210}+\frac{(1000-840)^2}{840}=507.93$
이 정도면 정말 말도 안되게 큰 값입니다.
즉, 독립이라는 가정 (Null 가정) 하에서 절대 나올 수 없는 값이므로 두 attribute가 서로 높은 correlation을 가진다고 할 수 있습니다.
🧩 이렇게 수식도 배우고, 예제로부터 chi-square test를 수행해보았습니다. 직접 하기에는 계산할 양이 적은 편은 아니고, attribute의 case가 늘어날수록 연산량이 늘어나겠지만, 우리의 주변에 있는 수많은 똑똑한 분들 덕분에 이를 컴퓨터에서 한번에 계산할 수 있는 라이브러리도 있고, 함수도 있습니다. 정말 멋지고 소중한 분들이라고 생각합니다(넙죽🙇♂️🙇♂️).
🧩 통계를 배운 분들이라면 아실 수 있겠지만, 통계에서의 카이제곱검정과 같은 의미를 가집니다. 다만 통계에서는 유의수준과 p-value를 통해서 주로 검정을 수행하지만, 오늘 배운 내용에서는 $χ^{2}$ 값을 직접 구해 correlation을 분석한다는 점이 살짝 다릅니다.
🧩 이번 포스팅에서는 categorical data를 위한 measure를 알아보았습니다. 다음 포스팅에서는 Numerical Data를 위한 방법들을 알아보도록 하겠습니다😀.
💡위 포스팅은 한국외국어대학교 바이오메디컬공학부 고윤희 교수님의 [생명정보학을 위한 데이터마이닝] 강의를 바탕으로 합니다.
'📌 데이터마이닝 > 데이터 전처리' 카테고리의 다른 글
| 🚩 데이터마이닝 12. Reduction - Nonlinear Regression (0) | 2023.02.17 |
|---|---|
| 🚩 데이터마이닝 11. Reduction - Linear Regression (0) | 2023.02.16 |
| 🚩 데이터마이닝 10. Data Reduction (0) | 2023.02.16 |
| 🚩 데이터마이닝 09. Integration-분산/상관관계분석 (0) | 2023.02.15 |
| 🚩 데이터마이닝 07. Data Cleaning (0) | 2023.02.11 |