모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

저번 포스팅을 통해 데이터의 dimension을 줄이는 Data Reduction의 종류에 대해 알아보았습니다.
이번에는 object를 줄이는 방법 중 하나인 Linear Regression에 대해서 알아보도록 합시다.
🚩 1. Parametric Data Reduction : Regression Analysis
데이터의 object를 줄이는 Numerosity Reduction에는 파라미터를 사용하는 방법과 사용하지 않는 방법이 있습니다.
알아볼 Linear Regression은 파라미터를 사용하는 방법이기에 Parametric Method가 무엇인지부터 간단히 알아봅시다.
그림을 보면 이해하시기 편할 것 같아서 그림을 하나 그려보았습니다.
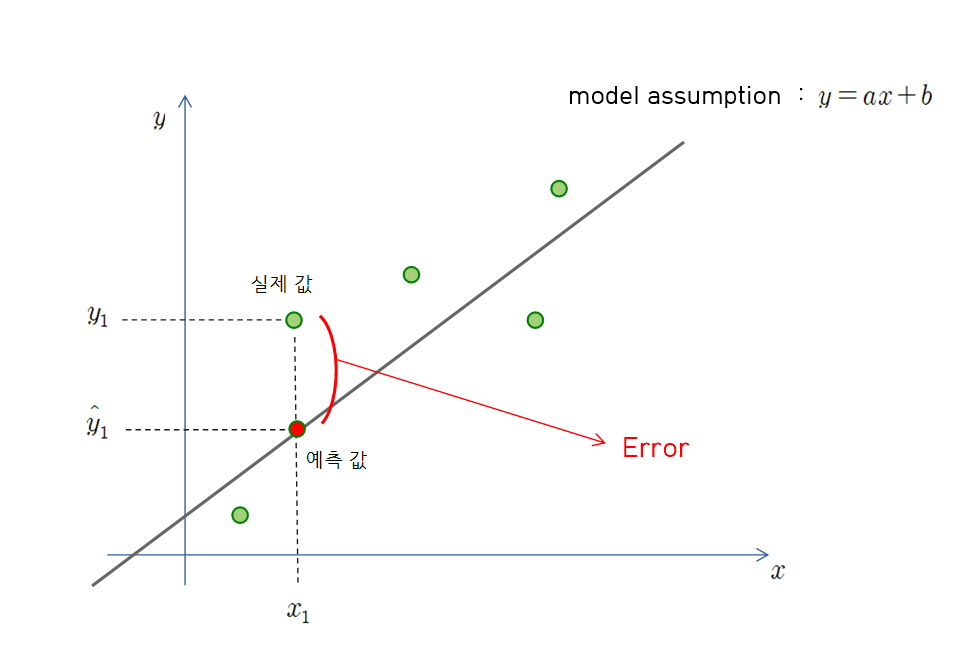
위 그림에서 우리의 데이터가 어떤 linaer 한 관계를 가지고 있을 거라고 가정하고, 그 모델을 $y=ax+b$ 라고 둡니다.
이어서 선언한 모델에 $x_1$ 이라는 독립변수를 대입하여 예측값 $\hat{y}_1$ 을 구합니다. 이후에는 종속변수 $x_1$ 에 대한 해당 데이터의 원래 값인 $y_1$ 와 예측값 $\hat{y}_1$ 사이의 Error를 줄여나가는 방향으로 parameter를 업데이트하며 모델을 결정합니다.
이 Error를 계산하는 방법에는 assumption model에 따라 여러가지 방법이 있습니다.
🚩 2. Linear Regression
위와 같은 방식으로 데이터 설명을 위한 최적의 모델을 찾아나가는데, 사용되는 가정의 종류에 따라 모델 형태가 달라집니다. 그리고 사용하는 모델의 형태가 위에서 든 예시처럼 선형적인 형태를 가지고 있다면, 저희는 이 예측 모델을 Linear Regression Model이라고 부를 수 있습니다. 즉, 독립변수 $x_1$ 와 종속변수 $y_1$ 사이에 선형적인 관계가 있다는 assumption 하에서 데이터를 설명하는 것입니다.
▪ assumption model : $Y=WX+b\;\;(y = \hat{β}_1x+\hat{β}_0)$
▪ 직선으로 표현되는 모델
▪ Parameter : $W,\;\,b\;\;(\hat{β}_1,\;\hat{β}_0)$
▪ Error Method : $Least-Squared\;Method\;(LSM)$
이름은 어려워 보이지만 동작하는 알고리즘은 위에서 말한 기본적인 원리를 벗어나지 않습니다. 가정에 의한 모델을 하나 만들고, 그에 대한 예측값을 구해 실제 값과의 Error를 계산한 뒤 오차를 최소화할수 있도록 파라미터를 업데이트하면 끝입니다. 다만 처음에 모델을 가정할 때 어느 정도는 데이터의 전체적인 개형과 비슷하게 가정해야 하며, Error를 계산하는 Method의 적절한 선택이 필요합니다.
위에서 봤듯이 Linear Regression에서는 주로 LSM 을 사용할 텐데, 이제는 이에 대해 알아보도록 합시다.
📝 $Least\;Squared\;Method\; :\; Residual\;Sum\;of\;Squares\;(RSS)$
$for\;\;y = \hat{β}_1x+\hat{β}_0,$
$RSS=E_1^2 + E_2^2+...+E_{n}^2\;=(y_1-(\hat{β}_1x_1+\hat{β}_0))^2+(y_2-(\hat{β}_1x_2+\hat{β}_0))^2+...+(y_n-(\hat{β}_1x_n+\hat{β}_0))^2$
위의 식을 천천히 살펴보면, 각 실제값과 예측값 사이의 Error 제곱의 합으로 model에 대한 전체 Error가 구해집니다.
최종적으로 이 Error를 최소화하는 파라미터를 찾아야 하는데, 그때 사용하는 방법은 아래와 같습니다.
📝 $Least\;Square\;Approach\;:\;Minimize\;RSS$
$\hat{β}_1=\frac{\sum{(x_i-\overline{x})(y_i-\overline{y})}}{\sum{(x_i-\overline{x})^2}}$
$\hat{β}_0=\overline{y}-\hat{β}_1\overline{x}$
위의 수식에서 $\overline{x}$ 와 $\overline{y}$ 는 각각 독립변수와 종속변수의 평균을 의미합니다. 즉 예측값에서 원래 데이터에 대한 정보를 빼는 연산을 바탕으로 파라미터를 업데이트합니다. 식은 복잡하지만, 그 의미와 연산 과정은 정말 간단한 원리로 구성되어 있는 것을 확인할 수 있습니다. 하지만 사람이 저 연산을 하기에는 양이 너무 많기에, 저희는 머신을 통해서 이 과정들을 수행할 수 있습니다.
Linear Regression은 아래 블로그에 더 자세하게 올려두었으니 링크를 참고하면 좋을 것 같습니다👍👍.
📝 머신러닝 - Linear Regression 포스팅 모음
머신러닝
🖌️데이터 시각화 / 📊데이터분석 / 🧬생명정보학 공부 블로그
nyamin9.github.io
🧩 다음 포스팅에서는 object를 줄이는 방법 중 두번째인 Nonparametric Method에 대해 알아보도록 하겠습니다🏃♂️🏃♂️.
💡위 포스팅은 한국외국어대학교 바이오메디컬공학부 고윤희 교수님의 [생명정보학을 위한 데이터마이닝] 강의를 바탕으로 합니다.
'📌 데이터마이닝 > 데이터 전처리' 카테고리의 다른 글
| 🚩 데이터마이닝 13. Reduction - Nonparametric (0) | 2023.02.17 |
|---|---|
| 🚩 데이터마이닝 12. Reduction - Nonlinear Regression (0) | 2023.02.17 |
| 🚩 데이터마이닝 10. Data Reduction (0) | 2023.02.16 |
| 🚩 데이터마이닝 09. Integration-분산/상관관계분석 (0) | 2023.02.15 |
| 🚩 데이터마이닝 08. Integration-카이제곱검정 (0) | 2023.02.14 |