모바일은 화면을 돌려 가로화면으로 보시는 게 읽으시기 편할 수 있습니다. 돌려서 보시는 걸 추천드릴게요!!

저번 포스팅에서는 범주형 데이터에 대한 data integration 방법인 chi-square test에 대해 알아보았습니다. 이번 포스팅에서는 Numerical Data, 즉 수치형 데이터에 대한 방법들을 알아보도록 합시다.
🧩 이 방법들은 아래와 같이 정리할 수 있습니다.
- 분산분석 (Variance)
- 공분산 분석 (Covariance)
- 상관관계 분석 (Correlation)
variance measure부터 차근차근 알아보도록 합시다.
🚩 1. Variance for single numerical data variable
분산, 즉 variance를 다루기 전에 평균과 관련된 기초적인 통계 관련 지식을 짚고 갈 필요가 있을 듯 합니다. 평균은 각 표본의 합을 표본의 수로 나눈 것을 의미하며, 보통 $E(X)$, $μ$ 라는 기호를 사용합니다. 사실 거창하게 통계 지식이라고 말은 해뒀지만, 평균만 알면 뒤에 나올 내용들을 이해하는 데에는 전혀 어려움이 없을 것이라 생각합니다. 또한 편차라는 개념도 있는데요, 편차는 관측값 - 평균 을 의미하며, 주로 $X - μ$ 라고 표현됩니다.
위의 두 개념을 사용하면 분산을 쉽게 설명할 수 있습니다.
분산은 편차제곱들의 평균으로 계산되며, 표본이 흩어진 정도를 의미합니다. 수식은 아래와 같습니다.
$σ^2 = Var(X) = E((X-μ)^2)=E(X^2)-(E(X))^2$
$if\;\,X\;\,is\;\,discrete,\;\;σ^2 =\sum{(X-μ)^2}f(X),\;\;\,and\;\,f(X):$ 확률질량함수
$if\;\,X\;\,is\;\,continuous,\;\;σ^2 =\int_{-\infty}^\infty{(X-μ)^2}f(X),\;\;\,and\;\,f(X):$ 확률밀도함수
위의 두 식에서 볼 수 있듯이 $X$라는 변수가 연속이냐, 불연속이냐에 따라 정의되는 확률 함수의 형태도 다르고 그 계산 방식도 다르기 때문에 이를 고려해줘야 합니다. 하지만 이를 데이터마이닝에서 설명하기에는 통계학 얘기가 길어길 것 같기 때문에, 나중에 기회가 되면 한번 정리하도록 하겠습니다.
이어서 표준편차, 즉 Standard Deviation를 구해줍니다. 표준편차는 분산에 제곱근을 취한 값이며, 수식은 아래와 같습니다.
$σ = \sqrt{σ^2}$
분산과 표준편차를 통해서 저희가 알고 싶은 value가 평균으로부터 얼마나 떨어져있는지를 확인하고, 그 데이터를 선택해도 될지, 통합해도 될지 여부를 알아낼 수 있습니다.
🚩 2. Covariance for two variables
앞서 살펴본 variance는 단일 variable의 데이터 분포를 알아보는 데에 사용했다면 이번에 알아볼 Covariacne, 즉 공분산분석은 두 variable 사이의 관계를 알아보기 위해 사용합니다. 수식은 아래와 같습니다.
$σ_{12} = E[(X_1-μ_1)(X_2-μ_2)] = E(X_1X_2)-μ_1μ_2=E(X_1X_2)-E(X_1)E(X_2)$
즉,
$σ_{12} = \frac{1}{n}\sum_{i=1}^n(X_{i1}-μ_1)(X_{i2}-μ_2)$
그리고 이때,
$if\;\;σ_{12}\,>\,0\;:\;positive\;covariance$
$if\;\;σ_{12}\,<\,0\;:\;negative\;covariance$
$if\;\,X_1,\,X2\;\,is\;\,independent\;\,for\;\,each\;\,other,\;\,σ_{12}\,=\,0$
예시를 한번 살펴보도록 합시다.
$$ex) (X_1,X_2)=(2,5)\;(3,8)\;(5,10)\;(4,11)\;(6,14)$$
$$X_1 = (2+3+5+4+6)/5=4,\;\;\;\;\;X_2=(5+8+10+11+14)/5=9.6$$
$$σ_{12} = 15×((2−4)(5−9.6)+(3−4)(8−9.6)+(5−4)(10−9.6)+(4−4)(11−9.6)+(6−4)(14−9.6))=4$$
$E(X_1X_2)−E(X_1)E(X_2)$ 공식을 사용해서 더 쉽게 구할 수도 있습니다.
$$σ_{12}=E(X_1X_2)−E(X_1)E(X_2)=(10+24+50+44+84)5−4×9.6=42.4−38.4=4$$
구한 공분산이 4로 0보다 크기 때문에 두 variable 은 서로 positive한 관계임을 알 수 있습니다.
이렇게 공분산을 통해 두 variable, 즉 attribute들 간의 관계를 알 수 있지만, 이는 단위의 영향을 받는다는 단점을 가지고 있습니다. 예를 들어 하나의 변수가 cm 단위이고 디른 변수는 m단위라고 가정하면, 공분산은 이를 보정해주는 역할은 해주지 못합니다. 이러한 이유로 다른 방법이 필요해졌고, 그렇게 나온 개념이 피어슨 상관계수입니다.
🚩 3. Correlation between two numerical variables
상관계수는 수식부터 먼저 살펴봅시다.
$ρ_{12} = \frac{σ_{12}}{σ_1σ_2} = \frac{\sum{(X_{i1}-μ_1)(X_{i2}-μ_2)}}{\sqrt{\sum{(X_{i1}-μ_1)^2(X_{i2}-μ_2)^2}}}$
위의 식만 보면 상당히 복잡해보이지만, 사실은 공분산을 표준편차1과 표준편차2의 곱으로 나눠줌으로써 정규화해주는 것입니다. 그리고 이 과정에서 분모와 분자의 단위가 약분이 되어 날아가므로 상관계수는 단위의 영향을 받지 않습니다.
상관계수의 성질은 아래와 같습니다.
▪ $\;\;-1\leqqρ_{12}\leqq1$
▪ $\;\;if\;\;ρ_{12}>0\;\,:\;\,positive\;\;correlation$
▪ $\;\;if\;\;ρ_{12}=0\;\,:\;\,independent\;\,for\;\,each\;\,other$
▪ $\;\;if\;\;ρ_{12}<0\;\,:\;\,negative\;\;correlation$
▪ 그리고 상관계수의 크기가 클수록 강한 상관관계가 있음을 의미합니다.
상관계수 또한 앞에서 다뤘던 다양한 measure들과 같이 각 프로그래밍 언어에 이미 만들어진 내부 라이브러리 함수가 있습니다. 학기 중에 수행한 데이터마이닝 프로젝트에서 해당 함수를 사용한 적이 있기 때문에, 함수의 출력결과를 보는 것으로 이번 포스팅을 마무리하도록 하겠습니다.
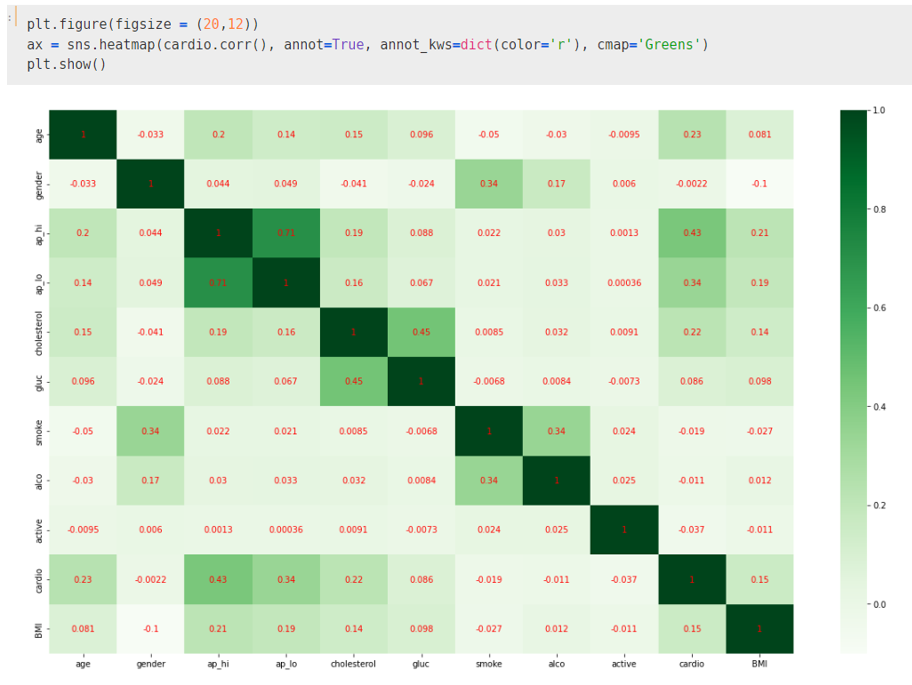
.corr 함수 를 통해 각 attribute 간의 상관계수를 계산해주고, seaborn 라이브러리를 사용해 시각화도 할 수 있습니다😊.
🚩 2022.09.08 추가 - correlation 은 수치형 변수와 수치형 변수 사이의 관계를 알아보기 위한 방법입니다. 저희는 프로젝트 진행 시에 범주형 변수간의 관계에 대해서도 상관관계 분석을 진행했기 때문에, 혹시 이 글을 읽으신 분들은 같은 실수를 저지르지 않았으면 합니다🤥. 범주형 변수 간의 상관관계 분석에는 Phi-correlation coefficient가 있다고 합니다. 나중에 한번 다뤄보겠습니다.
🧩 이렇게 해서 분산과 공분산, 그리고 상관계수에 이르는 내용들을 배웠습니다. 수식은 복잡하고 간단한 표본이라 해도 계산이 복잡한 경우가 많지만, 위의 함수처럼 편리한 함수가 많이 있기에 얘들을 잘 사용할 줄 아는 것이 더욱 중요할 것이라 생각합니다.
🧩 원래는 데이터마이닝 개념을 먼저 한번씩 살펴보고 프로젝트를 다룰 생각이었는데 이렇게 중간중간에 관련 결과를 넣는 것도 여러분의 이해에 도움이 될 것 같습니다. 앞으로는 다양한 자료를 사용해서 포스팅을 하도록 노력해봐야겠습니다.
🧩 이번 포스팅까지 해서 Data Integration은 한번씩 흝어봤습니다. 이제는 Data Reduction에 대해 배워보도록 합시다🏃♂️.
💡위 포스팅은 한국외국어대학교 바이오메디컬공학부 고윤희 교수님의 [생명정보학을 위한 데이터마이닝] 강의를 바탕으로 합니다.
'📌 데이터마이닝 > 데이터 전처리' 카테고리의 다른 글
| 🚩 데이터마이닝 12. Reduction - Nonlinear Regression (0) | 2023.02.17 |
|---|---|
| 🚩 데이터마이닝 11. Reduction - Linear Regression (0) | 2023.02.16 |
| 🚩 데이터마이닝 10. Data Reduction (0) | 2023.02.16 |
| 🚩 데이터마이닝 08. Integration-카이제곱검정 (0) | 2023.02.14 |
| 🚩 데이터마이닝 07. Data Cleaning (0) | 2023.02.11 |